LeetCode Notes

7. 整数反转

给你一个 32 位的有符号整数 x ，返回将 x 中的数字部分反转后的结果。

如果反转后整数超过 32 位的有符号整数的范围 [−231, 231 − 1] ，就返回 0。

假设环境不允许存储 64 位整数（有符号或无符号）。

示例 1：

输入：x = 123
输出：321

示例 2：

输入：x = -123
输出：-321

示例 3：

输入：x = 120
输出：21

示例 4：

输入：x = 0
输出：0

提示：

-231 <= x <= 231 - 1

Code1

240727

class Solution {
public:
    string str1 = "7463847412";
    string str2 = "-8463847412";
    int solve(int x) {
        int res = 0;
        while (x) {
            res *= 10;
            res += x % 10;
            x /= 10;
        }
        return res;
    }
    bool compare(string s1, string s2) { // s1是目标
        int len = s1.length();
        for (int i = len - 1; i >= 0; i--) {
            if (s1[i] > s2[i])
                return false;
            if (s1[i] < s2[i])
                return true;
        }
        return true;
    }
    int reverse(int x) {
        string xString = to_string(x);
        if (x == 0)
            return 0;
        else if (x < 0) {
            if (xString.length() > 11)
                return 0;
            else if (xString.length() == 11) {
                if (compare(xString, str2))
                    return solve(x);
                else
                    return 0;
            } else
                return solve(x);
        } else {
            if (xString.length() > 10)
                return 0;
            else if (xString.length() == 10) {
                if (compare(xString, str1))
                    return solve(x);
                else
                    return 0;
            } else
                return solve(x);
        }
    }
};
// 2147483647
//-2147483648

Code2

240727

class Solution:
    def reverse(self, x: int) -> int:
        res: int = 0
        flag:bool = False
        if(x<0):
            flag=True
            x=-x
        while x != 0:
            res *= 10
            res += x % 10
            x = x / 10
            x=int(x)
            print(res,x)
        if flag:
            res=-res
        if res>(1<<31)-1 or res<-(1<<31):
            return 0
        return res

8. 字符串转换整数 (atoi)

请你来实现一个 myAtoi(string s) 函数，使其能将字符串转换成一个 32 位有符号整数。

函数 myAtoi(string s) 的算法如下：

空格：读入字符串并丢弃无用的前导空格（" "）
符号：检查下一个字符（假设还未到字符末尾）为 '-' 还是 '+'。如果两者都不存在，则假定结果为正。
转换：通过跳过前置零来读取该整数，直到遇到非数字字符或到达字符串的结尾。如果没有读取数字，则结果为0。
舍入：如果整数数超过 32 位有符号整数范围 [−231, 231 − 1] ，需要截断这个整数，使其保持在这个范围内。具体来说，小于 −231 的整数应该被舍入为 −231 ，大于 231 − 1 的整数应该被舍入为 231 − 1 。

返回整数作为最终结果。

示例 1：

输入：s = "42"

输出：42

解释：加粗的字符串为已经读入的字符，插入符号是当前读取的字符。

带下划线线的字符是所读的内容，插入符号是当前读入位置。
第 1 步："42"（当前没有读入字符，因为没有前导空格）
         ^
第 2 步："42"（当前没有读入字符，因为这里不存在 '-' 或者 '+'）
         ^
第 3 步："42"（读入 "42"）
           ^

示例 2：

输入：s = " -042"

输出：-42

解释：

第 1 步："   -042"（读入前导空格，但忽视掉）
            ^
第 2 步："   -042"（读入 '-' 字符，所以结果应该是负数）
             ^
第 3 步："   -042"（读入 "042"，在结果中忽略前导零）
               ^

示例 3：

输入：s = "1337c0d3"

输出：1337

解释：

第 1 步："1337c0d3"（当前没有读入字符，因为没有前导空格）
         ^
第 2 步："1337c0d3"（当前没有读入字符，因为这里不存在 '-' 或者 '+'）
         ^
第 3 步："1337c0d3"（读入 "1337"；由于下一个字符不是一个数字，所以读入停止）
             ^

示例 4：

输入：s = "0-1"

输出：0

解释：

第 1 步："0-1" (当前没有读入字符，因为没有前导空格)
         ^
第 2 步："0-1" (当前没有读入字符，因为这里不存在 '-' 或者 '+')
         ^
第 3 步："0-1" (读入 "0"；由于下一个字符不是一个数字，所以读入停止)
          ^

示例 5：

输入：s = "words and 987"

输出：0

解释：

读取在第一个非数字字符“w”处停止。

提示：

0 <= s.length <= 200
s 由英文字母（大写和小写）、数字（0-9）、' '、'+'、'-' 和 '.' 组成

Code

240806

写这个逻辑好麻烦。补充点测试样例。

"42"
"   -042"
"1337c0d3"
"0-1"
"words and 987"
"-91283472332"
"+1"
"-+12"

class Solution {
public:
    int myAtoi(string s) {
        int res = 0;
        int len = s.length();
        int cur = 0;
        bool flag = false;
        while (cur < len && s[cur] == ' ')
            cur++;
        if (cur == len)
            return 0;
        if (s[cur] == '-') {
            flag = true;
            cur++;
        }else if (s[cur] == '+')
            cur++;
        while (cur < len && s[cur] <= '9' && s[cur] >= '0') {
            if (res > 214748364 || res<-214748364) {
                if (flag)
                    return -2147483648;
                else
                    return 2147483647;
                // res = res % 100000000;
            }
            if (res == 214748364 && !flag && s[cur] >= '8') {
                return 2147483647;
                // res = res % 100000000;
            }
            if (res == -214748364 && flag && s[cur] >= '9') {
                return -2147483648;
                // res = res % 100000000;
            }
            // try {
            //     res *= 10;
            // } catch (const exception& e) {
            //     cout << e.what() << endl;
            //     res = res % 100000000 * 10;
            // }
            res *= 10;
            if (flag)
                res -= s[cur] - '0';
            else 
                res += s[cur] - '0';
            cur++;
        }
        
        return res;
    }
};

9. 回文数

给你一个整数 x ，如果 x 是一个回文整数，返回 true ；否则，返回 false 。

回文数是指正序（从左向右）和倒序（从右向左）读都是一样的整数。

例如，121 是回文，而 123 不是。

示例 1：

输入：x = 121
输出：true

示例 2：

输入：x = -121
输出：false
解释：从左向右读, 为 -121 。 从右向左读, 为 121- 。因此它不是一个回文数。

示例 3：

输入：x = 10
输出：false
解释：从右向左读, 为 01 。因此它不是一个回文数。

提示：

-231 <= x <= 231 - 1

Code-cpp

240806

字符串做法

class Solution {
public:
    bool isPalindrome(int x) {
        string str = to_string(x);
        cout<<str<<endl;
        int r=str.length()-1;
        int l=0;
        while(l<r){
            if(str[l]!=str[r]) return false;
            l++;
            r--;
        }
        return true;
    }
};

纯数字做法

class Solution {
public:
    bool isPalindrome(int x) {
        if(x<0) return false;
        long long rev_num = 0;
        long long temp = x;
        while(temp){
            rev_num=rev_num*10+temp%10;
            temp/=10;
        }
        return x==rev_num;
    }
};

10. 正则表达式匹配

给你一个字符串 s 和一个字符规律 p，请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。

'.' 匹配任意单个字符
'*' 匹配零个或多个前面的那一个元素

所谓匹配，是要涵盖整个字符串 s 的，而不是部分字符串。

示例 1：

输入：s = "aa", p = "a"
输出：false
解释："a" 无法匹配 "aa" 整个字符串。

示例 2:

输入：s = "aa", p = "a*"
输出：true
解释：因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此，字符串 "aa" 可被视为 'a' 重复了一次。

示例 3：

输入：s = "ab", p = ".*"
输出：true
解释：".*" 表示可匹配零个或多个（'*'）任意字符（'.'）。

提示：

1 <= s.length <= 20
1 <= p.length <= 20
s 只包含从 a-z 的小写字母。
p 只包含从 a-z 的小写字母，以及字符 . 和 *。
保证每次出现字符 * 时，前面都匹配到有效的字符

Code-cpp-1

240807

632ms击败5.01%。时间感人。

class Solution {
public:
    int len_s, len_p, cur_s, cur_p, cur_arr;
    vector<string> arr;
    string str;
    bool isMatch(string s, string p) {
        len_s = s.length();
        len_p = p.length();
        cur_s = 0;
        cur_p = 0;
        cur_arr = 0;
        str = s;

        while (cur_p < len_p) {
            if (cur_p + 1 < len_p && p[cur_p + 1] == '*') {
                arr.push_back(string(1, p[cur_p]) + "*");
                cur_p += 2;
            } else {
                arr.push_back(string(1, p[cur_p]));
                cur_p++;
            }
        }
        for (auto& i : arr)
            cout << i << " ";
        cout << endl;
        return check(0, 0);
    }
    bool check(int _cur_s, int _cur_arr) {
        if (_cur_s == len_s && _cur_arr == arr.size())
            return true;
        if (_cur_arr >= arr.size())
            return false;
        if (_cur_s >= len_s) {
            while (_cur_arr < arr.size()) {
                if (arr[_cur_arr].length() == 1)
                    return false;
                _cur_arr++;
            }
            return true;
        }
        if (arr[_cur_arr].length() == 1) {
            if (arr[_cur_arr][0] == str[_cur_s])
                return check(_cur_s + 1, _cur_arr + 1);
            else if (arr[_cur_arr][0] == '.')
                return check(_cur_s + 1, _cur_arr + 1);
            else
                return false;
        } else {
            if (arr[_cur_arr][0] == '.') {
                while (_cur_s < len_s && !check(_cur_s, _cur_arr + 1)) {
                    _cur_s++;
                }
                return check(_cur_s, _cur_arr + 1);
            } else {
                if (check(_cur_s, _cur_arr + 1))
                    return true;
                while (_cur_s < len_s && str[_cur_s] == arr[_cur_arr][0]) {
                    // cout << _cur_s << " " << _cur_arr << endl;
                    if (check(_cur_s + 1, _cur_arr + 1))
                        return true;
                    else
                        _cur_s++;
                }
                return check(_cur_s, _cur_arr + 1);
            }
        }
    }
};

测试样例

"aa"
"a"
"aa"
"a*"
"ab"
".*"
"mississippi"
"mis*is*ip*."
"sip"
"s*p"
"a"
"ab*"
"bacaaabccbbccba"
".*..*c*a*.*b.b*c"

11. 盛最多水的容器

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

示例 1：

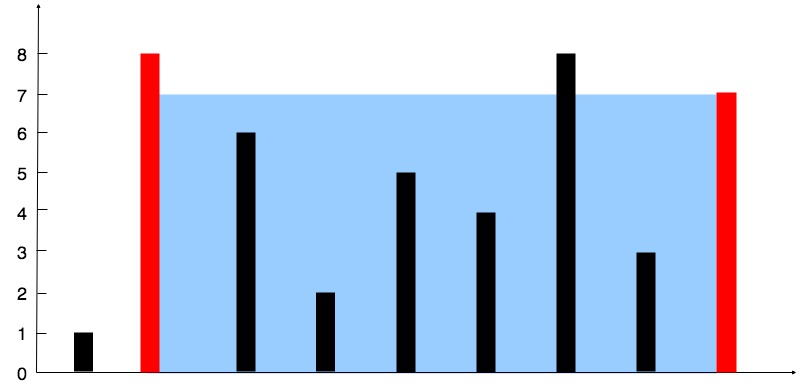
输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：

输入：height = [1,1]
输出：1

提示：

n == height.length
2 <= n <= 105
0 <= height[i] <= 104

Code-cpp

240808

时间复杂度\(O(NlogN)\)。

class Solution {
public:
    int maxArea(vector<int>& height) {
        int n=height.size();
        vector<pair<int,int>> vp;
        for(int i=0;i<n;i++){
            vp.emplace_back(make_pair(i,height[i]));
        }
        sort(vp.begin(),vp.end(),[&](const pair<int,int>& a,const pair<int,int>& b){
            return a.second>b.second;
        });
        // for(int i=0;i<n;i++){
        //     cout<<vp[i].second<<" ";
        // }
        int l=vp[0].first,r=vp[0].first;
        int Max=0;
        for(int i=1;i<n;i++){
            Max=max(Max,vp[i].second*max(abs(l-vp[i].first),abs(r-vp[i].first)));
            l=min(l,vp[i].first);
            r=max(r,vp[i].first);
            cout<<"l="<<l<<" r="<<r<<endl;
        }
        return Max;
    }
};

Code-cpp

240808

双指针法

class Solution {
public:
    int maxArea(vector<int>& height) {
        int l=0,r=height.size()-1;
        int Max=0;
        while(l<r){
            Max=max(Max,(r-l)*min(height[r],height[l]));
            if(height[l]<height[r]) l++;
            else r--;
        }
        return Max;
    }
};

12. 整数转罗马数字

七个不同的符号代表罗马数字，其值如下：

符号	值
I	1
V	5
X	10
L	50
C	100
D	500
M	1000

罗马数字是通过添加从最高到最低的小数位值的转换而形成的。将小数位值转换为罗马数字有以下规则：

如果该值不是以 4 或 9 开头，请选择可以从输入中减去的最大值的符号，将该符号附加到结果，减去其值，然后将其余部分转换为罗马数字。
如果该值以 4 或 9 开头，使用 减法形式，表示从以下符号中减去一个符号，例如 4 是 5 (V) 减 1 (I): IV ，9 是 10 (X) 减 1 (I)：IX。仅使用以下减法形式：4 (IV)，9 (IX)，40 (XL)，90 (XC)，400 (CD) 和 900 (CM)。
只有 10 的次方（I, X, C, M）最多可以连续附加 3 次以代表 10 的倍数。你不能多次附加 5 (V)，50 (L) 或 500 (D)。如果需要将符号附加4次，请使用 减法形式。

给定一个整数，将其转换为罗马数字。

示例 1：

输入：num = 3749

输出： "MMMDCCXLIX"

解释：

3000 = MMM 由于 1000 (M) + 1000 (M) + 1000 (M)
 700 = DCC 由于 500 (D) + 100 (C) + 100 (C)
  40 = XL 由于 50 (L) 减 10 (X)
   9 = IX 由于 10 (X) 减 1 (I)
注意：49 不是 50 (L) 减 1 (I) 因为转换是基于小数位

示例 2：

输入：num = 58

输出："LVIII"

解释：

50 = L
 8 = VIII

示例 3：

输入：num = 1994

输出："MCMXCIV"

解释：

1000 = M
 900 = CM
  90 = XC
   4 = IV

提示：

1 <= num <= 3999

Code

240811

class Solution {
public:
    string intToRoman(int num) {
        string str = to_string(num);
        string res = "";
        int len = str.length();
        if (len == 4) {
            char c = str[len - 4] - '0';
            while (c--)
                res += "M";
        }
        if (len >= 3) {
            char c = str[len - 3] - '0';
            if (c < 4)
                while (c--)
                    res += "C";
            else if (c == 4)
                res += "CD";
            else if (c == 5)
                res += "D";
            else if (c == 9)
                res += "CM";
            else {
                c -= 5;
                res += "D";
                while (c--)
                    res += "C";
            }
        }
        if (len >= 2) {
            char c = str[len - 2] - '0';
            if (c < 4)
                while (c--)
                    res += "X";
            else if (c == 4)
                res += "XL";
            else if (c == 5)
                res += "L";
            else if (c == 9)
                res += "XC";
            else {
                c -= 5;
                res += "L";
                while (c--)
                    res += "X";
            }
        }
        if (len >= 1) {
            char c = str[len - 1] - '0';
            if (c < 4)
                while (c--)
                    res += "I";
            else if (c == 4)
                res += "IV";
            else if (c == 5)
                res += "V";
            else if (c == 9)
                res += "IX";
            else {
                c -= 5;
                res += "V";
                while (c--)
                    res += "I";
            }
        }
        return res;
    }
};

13. 罗马数字转整数

罗马数字包含以下七种字符: I， V， X， L，C，D 和 M。

字符          数值
I             1
V             5
X             10
L             50
C             100
D             500
M             1000

例如，罗马数字 2 写做 II ，即为两个并列的 1 。12 写做 XII ，即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。

通常情况下，罗马数字中小的数字在大的数字的右边。但也存在特例，例如 4 不写做 IIII，而是 IV。数字 1 在数字 5 的左边，所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地，数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况：

I 可以放在 V (5) 和 X (10) 的左边，来表示 4 和 9。
X 可以放在 L (50) 和 C (100) 的左边，来表示 40 和 90。
C 可以放在 D (500) 和 M (1000) 的左边，来表示 400 和 900。

给定一个罗马数字，将其转换成整数。

示例 1:

输入: s = "III"
输出: 3

示例 2:

输入: s = "IV"
输出: 4

示例 3:

输入: s = "IX"
输出: 9

示例 4:

输入: s = "LVIII"
输出: 58
解释: L = 50, V= 5, III = 3.

示例 5:

输入: s = "MCMXCIV"
输出: 1994
解释: M = 1000, CM = 900, XC = 90, IV = 4.

提示：

1 <= s.length <= 15
s 仅含字符 ('I', 'V', 'X', 'L', 'C', 'D', 'M')
题目数据保证 s 是一个有效的罗马数字，且表示整数在范围 [1, 3999] 内
题目所给测试用例皆符合罗马数字书写规则，不会出现跨位等情况。
IL 和 IM 这样的例子并不符合题目要求，49 应该写作 XLIX，999 应该写作 CMXCIX 。
关于罗马数字的详尽书写规则，可以参考罗马数字 - 百度百科。

Code

240811

class Solution {
public:
    int romanToInt(string s) {
        map<char, int> m = {{'M', 1000}, {'C', 100}, {'D', 500}, {'L', 50},
                            {'X', 10},   {'V', 5},   {'I', 1}};
        int len = s.length();
        int res = 0;
        for(int i=0;i<len;i++){
            if(i+1<len && m[s[i]]<m[s[i+1]]){
                res+=m[s[i+1]]-m[s[i]];
                i++;
            }else{
                res+=m[s[i]];
            }
            // cout<<i+1<<" "<<res<<endl;
        }
        return res;
    }
};

14. 最长公共前缀

编写一个函数来查找字符串数组中的最长公共前缀。

如果不存在公共前缀，返回空字符串 ""。

示例 1：

输入：strs = ["flower","flow","flight"]
输出："fl"

示例 2：

输入：strs = ["dog","racecar","car"]
输出：""
解释：输入不存在公共前缀。

提示：

1 <= strs.length <= 200
0 <= strs[i].length <= 200
strs[i] 仅由小写英文字母组成

Code

240811

class Solution {
public:
    string longestCommonPrefix(vector<string>& strs) {
        string res = "";
        for(int i=0;i<strs[0].length();i++){
            for(int j=1;j<strs.size();j++){
                if(strs[j].length()<i || strs[j][i]!=strs[0][i])
                    return res;
            }
            res+=strs[0][i];
        }
        return res;
    }
};

15. 三数之和

给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请你返回所有和为 0 且不重复的三元组。

注意：答案中不可以包含重复的三元组。

示例 1：

输入：nums = [-1,0,1,2,-1,-4]
输出：[[-1,-1,2],[-1,0,1]]
解释：
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意，输出的顺序和三元组的顺序并不重要。

示例 2：

输入：nums = [0,1,1]
输出：[]
解释：唯一可能的三元组和不为 0 。

示例 3：

输入：nums = [0,0,0]
输出：[[0,0,0]]
解释：唯一可能的三元组和为 0 。

提示：

3 <= nums.length <= 3000
-105 <= nums[i] <= 105

Code

240811

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        vector<vector<int>> vv;
        sort(nums.begin(), nums.end(),
             [](const int& a, const int& b) { return a < b; });
        int len = nums.size();
        for (int i = 0; i < len - 2; i++) {
            if (i && nums[i] == nums[i - 1])
                continue;
            int l = i + 1;
            int r = len - 1;
            while (l < r) {
                if (nums[i] + nums[l] + nums[r] < 0)
                    // do
                    l++;
                // while (l + 1 < len && nums[l + 1] == nums[l]);
                else if (nums[i] + nums[l] + nums[r] > 0)
                    // do
                    r--;
                // while (r - 1 >= 0 && nums[r - 1] == nums[r]);
                else {
                    vv.emplace_back(vector<int>{nums[i], nums[l], nums[r]});
                    // do
                    l++;
                    // while (l + 1 < len && nums[l + 1] == nums[l]);
                    // do
                    r--;
                    // while (r - 1 >= 0 && nums[r - 1] == nums[r]);
                }
            }
        }
        auto last = unique(vv.begin(), vv.end());
        cout << last - vv.begin() << endl;
        vv.erase(last, vv.end());
        return vv;
    }
};

16. 最接近的三数之和

给你一个长度为 n 的整数数组 nums 和一个目标值 target。请你从 nums 中选出三个整数，使它们的和与 target 最接近。

返回这三个数的和。

假定每组输入只存在恰好一个解。

示例 1：

输入：nums = [-1,2,1,-4], target = 1
输出：2
解释：与 target 最接近的和是 2 (-1 + 2 + 1 = 2)。

示例 2：

输入：nums = [0,0,0], target = 1
输出：0
解释：与 target 最接近的和是 0（0 + 0 + 0 = 0）。

提示：

3 <= nums.length <= 1000
-1000 <= nums[i] <= 1000
-104 <= target <= 104

Code

240812

class Solution {
public:
    int threeSumClosest(vector<int>& nums, int target) {
        sort(nums.begin(), nums.end());
        int len = nums.size();
        int res = nums[0]+nums[1]+nums[len-1];
        for (int i = 0; i < len - 2; i++) {
            int l = i + 1, r = len - 1;
            while (l < r) {
                if (abs(nums[i] + nums[l] + nums[r] - target) <
                    abs(res - target)) {
                    res = nums[i] + nums[l] + nums[r];
                }
                if (abs(nums[i] + nums[l + 1] + nums[r] - target) <
                    abs(nums[i] + nums[l] + nums[r - 1] - target))
                    l++;
                else
                    r--;
            }
        }
        return res;
    }
};

Code2

240812

优化的写法

class Solution {
public:
    int threeSumClosest(vector<int>& nums, int target) {
        sort(nums.begin(), nums.end());
        int len = nums.size();
        int res = nums[0] + nums[1] + nums[len - 1];
        for (int i = 0; i < len - 2; i++) {
            int l = i + 1, r = len - 1;
            while (l < r) {
                if (abs(nums[i] + nums[l] + nums[r] - target) <
                    abs(res - target)) {
                    res = nums[i] + nums[l] + nums[r];
                }
                if (nums[i] + nums[l] + nums[r] > target)
                    r--;
                else
                    l++;
            }
        }
        return res;
    }
};

17. 电话号码的字母组合

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

示例 1：

输入：digits = "23"
输出：["ad","ae","af","bd","be","bf","cd","ce","cf"]

示例 2：

输入：digits = ""
输出：[]

示例 3：

输入：digits = "2"
输出：["a","b","c"]

提示：

0 <= digits.length <= 4
digits[i] 是范围 ['2', '9'] 的一个数字。

Code

240813

class Solution {
public:
    vector<string> letterCombinations(string digits) {
        vector<string> vs, temp;
        map<char, vector<char>> mv{
            {'2', {'a', 'b', 'c'}}, {'3', {'d', 'e', 'f'}},
            {'4', {'g', 'h', 'i'}}, {'5', {'j', 'k', 'l'}},
            {'6', {'m', 'n', 'o'}}, {'7', {'p', 'q', 'r', 's'}},
            {'8', {'t', 'u', 'v'}}, {'9', {'w', 'x', 'y', 'z'}}};
        int len = digits.length();
        if (len == 0)
            return vs;
        vs.emplace_back("");
        for (int i = 0; i < len; i++) {
            temp.clear();
            for (auto& j : vs) {
                for (auto& k : mv[digits[i]])
                    temp.emplace_back(j + string(1, k));
            }
            swap(temp,vs);
        }
        return vs;
    }
};

18. 四数之和

给你一个由 n 个整数组成的数组 nums ，和一个目标值 target 。请你找出并返回满足下述全部条件且不重复的四元组 [nums[a], nums[b], nums[c], nums[d]] （若两个四元组元素一一对应，则认为两个四元组重复）：

0 <= a, b, c, d < n
a、b、c 和 d 互不相同
nums[a] + nums[b] + nums[c] + nums[d] == target

你可以按 任意顺序 返回答案。

示例 1：

输入：nums = [1,0,-1,0,-2,2], target = 0
输出：[[-2,-1,1,2],[-2,0,0,2],[-1,0,0,1]]

示例 2：

输入：nums = [2,2,2,2,2], target = 8
输出：[[2,2,2,2]]

提示：

1 <= nums.length <= 200
-109 <= nums[i] <= 109
-109 <= target <= 109

Code

240813

好麻烦啊，感觉比官方题解多了很多特判的地方。有个样例还卡io时间（还好把cout注释掉了）

样例：

[1,0,-1,0,-2,2]
0
[2,2,2,2,2]
8
[-2,-1,-1,1,1,2,2]
0
[0,0,0,0]
0
[-3,-2,-1,0,0,1,2,3]
0
[1000000000,1000000000,1000000000,1000000000]
0

class Solution {
public:
    vector<vector<int>> fourSum(vector<int>& nums, int target) {
        vector<vector<int>> vv;
        sort(nums.begin(), nums.end());
        // for (auto& num : nums)
        //     cout << num << " ";
        // cout << endl;
        int len = nums.size();
        for (int a = 0; a < len; a++) {
            if (a > 0 && nums[a] == nums[a - 1])
                continue;
            bool flag = true;
            for (int b = a + 1; b < len; b++) {
                if (flag)
                    flag = false;
                else
                    while (b < len && b >= 1 && nums[b - 1] == nums[b])
                        b++;
                int l = b + 1, r = len - 1;
                while (l < r) {
                    // cout << a << " " << b << " " << l << " " << r << endl;
                    if ((long long)nums[a] + nums[b] + nums[l] + nums[r] ==
                        target) {
                        vv.emplace_back(
                            vector<int>{nums[a], nums[b], nums[l], nums[r]});
                        l++;
                        r--;
                    } else if ((long long)nums[a] + nums[b] + nums[l] +
                                   nums[r] <
                               target) {
                        l++;
                    } else {
                        r--;
                    }
                    while (l < r && nums[l - 1] == nums[l] && l - 1 != b)
                        l++;
                    while (r + 1 < len && r >= 0 && nums[r] == nums[r + 1])
                        r--;
                }
            }
        }
        return vv;
    }
};

class Solution {
public:
    vector<vector<int>> fourSum(vector<int>& nums, int target) {
        vector<vector<int>> vv;
        sort(nums.begin(), nums.end());
        int len = nums.size();
        for (int a = 0; a < len; a++) {
            if (a && nums[a] == nums[a - 1])
                continue;
            for (int b = a + 1; b < len; b++) {
                while (b < len && b != a + 1 && nums[b - 1] == nums[b])
                    b++;
                int l = b + 1, r = len - 1;
                while (l < r) {
                    if ((long long)nums[a] + nums[b] + nums[l] + nums[r] == target) {
                        vv.emplace_back(vector<int>{nums[a], nums[b], nums[l], nums[r]});
                        l++;
                        r--;
                    } else if ((long long)nums[a] + nums[b] + nums[l] + nums[r] < target)
                        l++;
                    else
                        r--;
                    while (l - 1 != b && l < len && nums[l - 1] == nums[l])
                        l++;
                    while (r >= 0 && r + 1 < len && nums[r] == nums[r + 1])
                        r--;
                }
            }
        }
        return vv;
    }
};

19. 删除链表的倒数第 N 个结点

给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

示例 1：

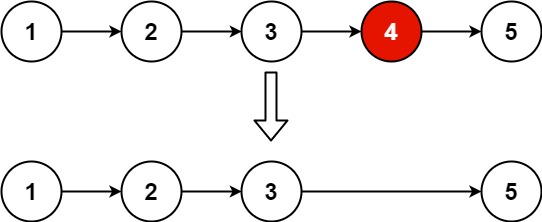
输入：head = [1,2,3,4,5], n = 2
输出：[1,2,3,5]

示例 2：

输入：head = [1], n = 1
输出：[]

示例 3：

输入：head = [1,2], n = 1
输出：[1]

提示：

链表中结点的数目为 sz
1 <= sz <= 30
0 <= Node.val <= 100
1 <= n <= sz

进阶：你能尝试使用一趟扫描实现吗？

Code

240813

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        ListNode* p1 = head;
        ListNode* p2 = head;
        int len = 0;
        while (p2 != nullptr) {
            len++;
            p2 = p2->next;
        }
        cout << len << endl;
        n = len - n - 1;
        cout << n << endl;
        if (n == -1)
            return head->next;
        while (n--) {
            p1 = p1->next;
        }
        p1->next = p1->next->next;
        return head;
    }
};

20. 有效的括号

给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
每个右括号都有一个对应的相同类型的左括号。

示例 1：

输入：s = "()"
输出：true

示例 2：

输入：s = "()[]{}"
输出：true

示例 3：

输入：s = "(]"
输出：false

提示：

1 <= s.length <= 104
s 仅由括号 '()[]{}' 组成

Code

240813

class Solution {
public:
    bool isValid(string s) {
        stack<char> stk;
        for (auto& i : s) {
            if (i == '(' || i == '[' || i == '{')
                stk.push(i);
            else {
                if (stk.size() == 0)
                    return false;
                char top = stk.top();
                stk.pop();
                if (top == '(' && i == ')')
                    continue;
                else if (top == '[' && i == ']')
                    continue;
                else if (top == '{' && i == '}')
                    continue;
                else
                    return false;
            }
        }
        if (stk.size() == 0)
            return true;
        else
            return false;
    }
};

21. 合并两个有序链表

将两个升序链表合并为一个新的升序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

示例 1：

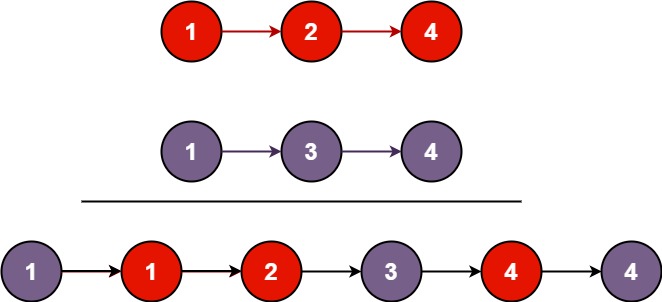
输入：l1 = [1,2,4], l2 = [1,3,4]
输出：[1,1,2,3,4,4]

示例 2：

输入：l1 = [], l2 = []
输出：[]

示例 3：

输入：l1 = [], l2 = [0]
输出：[0]

提示：

两个链表的节点数目范围是 [0, 50]
-100 <= Node.val <= 100
l1 和 l2 均按 非递减顺序 排列

Code

240814

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
        ListNode* head=new ListNode();
        ListNode* cur=head;
        while(list1!=nullptr && list2!=nullptr){
            if(list1->val<list2->val){
                cur->next = new ListNode(list1->val);
                list1=list1->next;
            }else{
                cur->next = new ListNode(list2->val);
                list2=list2->next;
            }
            cur=cur->next;
        }
        while(list1!=nullptr){
            cur->next = new ListNode(list1->val);
            list1=list1->next;
            cur=cur->next;
        }
        while(list2!=nullptr){
            cur->next = new ListNode(list2->val);
            list2=list2->next;
            cur=cur->next;
        }
        return head->next;
    }
};

23. 合并 K 个升序链表

给你一个链表数组，每个链表都已经按升序排列。

请你将所有链表合并到一个升序链表中，返回合并后的链表。

示例 1：

输入：lists = [[1,4,5],[1,3,4],[2,6]]
输出：[1,1,2,3,4,4,5,6]
解释：链表数组如下：
[
  1->4->5,
  1->3->4,
  2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6

示例 2：

输入：lists = []
输出：[]

示例 3：

输入：lists = [[]]
输出：[]

提示：

k == lists.length
0 <= k <= 10^4
0 <= lists[i].length <= 500
-10^4 <= lists[i][j] <= 10^4
lists[i] 按升序排列
lists[i].length 的总和不超过 10^4

Code

240818

使用遍历，\(O(n^2)\)

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        ListNode* head = new ListNode(-0x3f3f3f3f);
        ListNode* res_cur = head;
        // bool flag = true;
        int size = lists.size();
        while (true) {
            int temp_min = 0x3f3f3f3f;
            int temp_cur = -1;
            for (int i = 0; i < size; i++) {
                if (lists[i] && lists[i]->val < temp_min) {
                    temp_min = lists[i]->val;
                    temp_cur = i;
                }
            }
            if (temp_cur == -1)
                break;
            res_cur->next = new ListNode(temp_min);
            res_cur = res_cur->next;
            lists[temp_cur] = lists[temp_cur]->next;
        }
        return head->next;
    }
};

24. 两两交换链表中的节点

给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）。

示例 1：

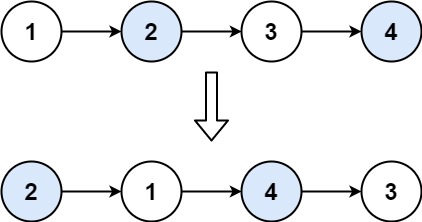
输入：head = [1,2,3,4]
输出：[2,1,4,3]

示例 2：

输入：head = []
输出：[]

示例 3：

输入：head = [1]
输出：[1]

提示：

链表中节点的数目在范围 [0, 100] 内
0 <= Node.val <= 100

Code

240820

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        if (head == nullptr)
            return nullptr;
        if (head->next == nullptr)
            return head;
        ListNode *cur1, *cur2, *temp = new ListNode();
        ListNode* result_head = temp;
        cur1 = head;
        while (cur1 != nullptr && cur1->next != nullptr) {
            cur2 = cur1->next;
            cur1->next = cur2->next;
            cur2->next = cur1;
            temp->next = cur2;
            temp = cur1;
            cur1 = cur1->next;
        }
        return result_head->next;
    }
};

25. K 个一组翻转链表

给你链表的头节点 head ，每 k 个节点一组进行翻转，请你返回修改后的链表。

k 是一个正整数，它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍，那么请将最后剩余的节点保持原有顺序。

你不能只是单纯的改变节点内部的值，而是需要实际进行节点交换。

示例 1：

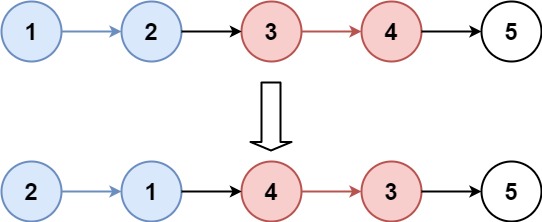
输入：head = [1,2,3,4,5], k = 2
输出：[2,1,4,3,5]

示例 2：

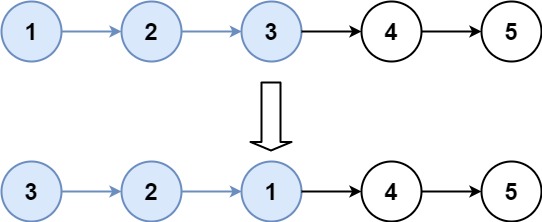
输入：head = [1,2,3,4,5], k = 3
输出：[3,2,1,4,5]

提示：

链表中的节点数目为 n
1 <= k <= n <= 5000
0 <= Node.val <= 1000

进阶：你可以设计一个只用 O(1) 额外内存空间的算法解决此问题吗？

Code

240820

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    void reverse(ListNode* cur1, ListNode* cur2) {
        // if (cur1 == cur2)
        //     return;
        ListNode *tmp1 = cur1->next, *tmp2 = cur2->next;
        cur1->next = tmp2;
        cur2->next = tmp1;
        swap(tmp1->next, tmp2->next);
    }
    void print(ListNode* cur) {
        while (cur) {
            cout << cur->val << " ";
            cur = cur->next;
        }
        cout << endl;
    }
    ListNode* reverseKGroup(ListNode* head, int k) {
        ListNode* res = new ListNode();
        ListNode* cur = res;
        res->next = head;
        vector<ListNode*> vec(k);
        while (true) {
            ListNode* temp = cur->next;
            for (int i = 0; i < k; i++) {
                if (temp != nullptr)
                    temp = temp->next;
                else
                    return res->next;
            }
            for (int i = 0; i < k / 2; i++) {
                ListNode* l = cur;
                ListNode* r = cur;
                for (int j = 0; j < i; j++)
                    l = l->next;
                for (int j = 0; j < k - i - 1; j++)
                    r = r->next;
                reverse(l, r);
            }
            // // cur = cur->next;
            // for (int i = 0, j = k - 1; i < j; i++, j--) {
            //     reverse(vec[i], vec[j]);
            //     print(res);
            // }
            for (int i = 0; i < k; i++)
                cur = cur->next;
            if (cur == nullptr)
                return res->next;
        }
        return res->next;
    }
};

26. 删除有序数组中的重复项

给你一个 非严格递增排列 的数组 nums ，请你原地删除重复出现的元素，使每个元素 只出现一次 ，返回删除后数组的新长度。元素的 相对顺序 应该保持一致。然后返回 nums 中唯一元素的个数。

考虑 nums 的唯一元素的数量为 k ，你需要做以下事情确保你的题解可以被通过：

更改数组 nums ，使 nums 的前 k 个元素包含唯一元素，并按照它们最初在 nums 中出现的顺序排列。nums 的其余元素与 nums 的大小不重要。
返回 k 。

判题标准:

系统会用下面的代码来测试你的题解:

int[] nums = [...]; // 输入数组
int[] expectedNums = [...]; // 长度正确的期望答案

int k = removeDuplicates(nums); // 调用

assert k == expectedNums.length;
for (int i = 0; i < k; i++) {
    assert nums[i] == expectedNums[i];
}

如果所有断言都通过，那么您的题解将被通过。

示例 1：

输入：nums = [1,1,2]
输出：2, nums = [1,2,_]
解释：函数应该返回新的长度 2 ，并且原数组 nums 的前两个元素被修改为 1, 2 。不需要考虑数组中超出新长度后面的元素。

示例 2：

输入：nums = [0,0,1,1,1,2,2,3,3,4]
输出：5, nums = [0,1,2,3,4]
解释：函数应该返回新的长度 5 ， 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4 。不需要考虑数组中超出新长度后面的元素。

提示：

1 <= nums.length <= 3 * 104
-104 <= nums[i] <= 104
nums 已按 非严格递增 排列

Code

240905

class Solution {
public:
    int removeDuplicates(vector<int>& nums) {
        int vis[20010];
        memset(vis,0,sizeof(vis));
        int cur=0;
        int size=nums.size();
        for(int i=0;i<size;i++){
            if(!vis[nums[i]+10000]){
                vis[nums[i]+10000]=1;
                nums[cur]=nums[i];
                cur++;
            }
        }
        return cur;
    }
};

27. 移除元素

简单

给你一个数组 nums 和一个值 val，你需要原地移除所有数值等于 val 的元素。元素的顺序可能发生改变。然后返回 nums 中与 val 不同的元素的数量。

假设 nums 中不等于 val 的元素数量为 k，要通过此题，您需要执行以下操作：

更改 nums 数组，使 nums 的前 k 个元素包含不等于 val 的元素。nums 的其余元素和 nums 的大小并不重要。
返回 k。

用户评测：

评测机将使用以下代码测试您的解决方案：

int[] nums = [...]; // 输入数组
int val = ...; // 要移除的值
int[] expectedNums = [...]; // 长度正确的预期答案。
                            // 它以不等于 val 的值排序。

int k = removeElement(nums, val); // 调用你的实现

assert k == expectedNums.length;
sort(nums, 0, k); // 排序 nums 的前 k 个元素
for (int i = 0; i < actualLength; i++) {
    assert nums[i] == expectedNums[i];
}

如果所有的断言都通过，你的解决方案将会通过。

示例 1：

输入：nums = [3,2,2,3], val = 3
输出：2, nums = [2,2,_,_]
解释：你的函数函数应该返回 k = 2, 并且 nums 中的前两个元素均为 2。
你在返回的 k 个元素之外留下了什么并不重要（因此它们并不计入评测）。

示例 2：

输入：nums = [0,1,2,2,3,0,4,2], val = 2
输出：5, nums = [0,1,4,0,3,_,_,_]
解释：你的函数应该返回 k = 5，并且 nums 中的前五个元素为 0,0,1,3,4。
注意这五个元素可以任意顺序返回。
你在返回的 k 个元素之外留下了什么并不重要（因此它们并不计入评测）。

提示：

0 <= nums.length <= 100
0 <= nums[i] <= 50
0 <= val <= 100

Code

240905

class Solution {
public:
    int removeElement(vector<int>& nums, int val) {
        int cur=0;
        int size=nums.size();
        for(int i=0;i<size;i++){
            if(nums[i]!=val){
                nums[cur]=nums[i];
                cur++;
            }
        }
        return cur;
    }
};

28. 找出字符串中第一个匹配项的下标

简单

给你两个字符串 haystack 和 needle ，请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标（下标从 0 开始）。如果 needle 不是 haystack 的一部分，则返回 -1 。

示例 1：

输入：haystack = "sadbutsad", needle = "sad"
输出：0
解释："sad" 在下标 0 和 6 处匹配。
第一个匹配项的下标是 0 ，所以返回 0 。

示例 2：

输入：haystack = "leetcode", needle = "leeto"
输出：-1
解释："leeto" 没有在 "leetcode" 中出现，所以返回 -1 。

提示：

1 <= haystack.length, needle.length <= 104
haystack 和 needle 仅由小写英文字符组成

Code

240905

class Solution {
public:
    int strStr(string haystack, string needle) {
        int h_len = haystack.length();
        int n_len = needle.length();
        for (int i = 0; i < h_len; i++) {
            if (haystack[i] != needle[0])
                continue;
            int j = 1;
            for (; j < n_len; j++) {
                if (haystack[i + j] != needle[j])
                    break;
            }
            if (j == n_len)
                return i;
        }
        return -1;
    }
};

31. 下一个排列

中等

整数数组的一个排列就是将其所有成员以序列或线性顺序排列。

例如，arr = [1,2,3] ，以下这些都可以视作 arr 的排列：[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。

整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。更正式地，如果数组的所有排列根据其字典顺序从小到大排列在一个容器中，那么数组的 下一个排列就是在这个有序容器中排在它后面的那个排列。如果不存在下一个更大的排列，那么这个数组必须重排为字典序最小的排列（即，其元素按升序排列）。

例如，arr = [1,2,3] 的下一个排列是 [1,3,2] 。
类似地，arr = [2,3,1] 的下一个排列是 [3,1,2] 。
而 arr = [3,2,1] 的下一个排列是 [1,2,3] ，因为 [3,2,1] 不存在一个字典序更大的排列。

给你一个整数数组 nums ，找出 nums 的下一个排列。

必须原地修改，只允许使用额外常数空间。

示例 1：

输入：nums = [1,2,3]
输出：[1,3,2]

示例 2：

输入：nums = [3,2,1]
输出：[1,2,3]

示例 3：

输入：nums = [1,1,5]
输出：[1,5,1]

提示：

1 <= nums.length <= 100
0 <= nums[i] <= 100

Code

240906

方法：以[1,3,4,2]举例。从右到左，找到第一个变小的数对，即(3,4)。将这个数对中右边的数标记为cur，我们需要从cur到数组末尾的这些数中找到，比cur-1这个数大且最接近的数。然后我们交换这两个数，再将cur到数组末尾用sort函数从小到大排序即可。

class Solution {
public:
    void nextPermutation(vector<int>& nums) {
        int size=nums.size();
        int cur=size-1;
        while(cur!=0 && nums[cur-1]>=nums[cur]) cur--;
        if(cur==0){
            sort(nums.begin(),nums.end());
        }else{
            cout<<cur<<endl;
            int min=cur;
            for(int i=cur+1;i<size;i++){
                if(nums[i]<nums[min] && nums[i]>nums[cur-1]) min=i;
            }
            swap(nums[min],nums[cur-1]);
            sort(nums.begin()+cur,nums.end());
        }
    }
};

36. 有效的数独

中等

请你判断一个 9 x 9 的数独是否有效。只需要 根据以下规则 ，验证已经填入的数字是否有效即可。

数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。（请参考示例图）

注意：

一个有效的数独（部分已被填充）不一定是可解的。
只需要根据以上规则，验证已经填入的数字是否有效即可。
空白格用 '.' 表示。

示例 1：

输入：board = 
[["5","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
输出：true

示例 2：

输入：board = 
[["8","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
输出：false
解释：除了第一行的第一个数字从 5 改为 8 以外，空格内其他数字均与 示例1 相同。 但由于位于左上角的 3x3 宫内有两个 8 存在, 因此这个数独是无效的。

提示：

board.length == 9
board[i].length == 9
board[i][j] 是一位数字（1-9）或者 '.'

Code

240906

只要大暴力就好了，没有别的解法

class Solution {
public:
    bool isValidSudoku(vector<vector<char>>& board) {
        int vis[10];
        for(int i=0;i<9;i++){
            memset(vis,0,sizeof(vis));
            for(int j=0;j<9;j++){
                if(board[i][j]!='.'){
                    vis[board[i][j]-'0']++;
                }
            }
            for(int j=1;j<10;j++){
                if(vis[j]>1) return false;
            }
        }
        for(int i=0;i<9;i++){
            memset(vis,0,sizeof(vis));
            for(int j=0;j<9;j++){
                if(board[j][i]!='.'){
                    vis[board[j][i]-'0']++;
                }
            }
            for(int j=1;j<10;j++){
                if(vis[j]>1) return false;
            }
        }
        int direction_x[]={0,0,0,1,1,1,2,2,2};
        int direction_y[]={0,1,2,0,1,2,0,1,2};
        for(int i=0;i<3;i++){
            for(int j=0;j<3;j++){
                memset(vis,0,sizeof(vis));
                for(int k=0;k<9;k++){
                    if(board[i*3+direction_x[k]][j*3+direction_y[k]]!='.')
                        vis[board[i*3+direction_x[k]][j*3+direction_y[k]]-'0']++;
                }
                for(int k=1;k<10;k++){
                    if(vis[k]>1) return false;
                }
            }
        }
        return true;
    }
};

38. 外观数列

中等

「外观数列」是一个数位字符串序列，由递归公式定义：

countAndSay(1) = "1"
countAndSay(n) 是 countAndSay(n-1) 的行程长度编码。

行程长度编码（RLE）是一种字符串压缩方法，其工作原理是通过将连续相同字符（重复两次或更多次）替换为字符重复次数（运行长度）和字符的串联。例如，要压缩字符串 "3322251" ，我们将 "33" 用 "23" 替换，将 "222" 用 "32" 替换，将 "5" 用 "15" 替换并将 "1" 用 "11" 替换。因此压缩后字符串变为 "23321511"。

给定一个整数 n ，返回 外观数列 的第 n 个元素。

示例 1：

输入：n = 4

输出："1211"

解释：

countAndSay(1) = "1"

countAndSay(2) = "1" 的行程长度编码 = "11"

countAndSay(3) = "11" 的行程长度编码 = "21"

countAndSay(4) = "21" 的行程长度编码 = "1211"

示例 2：

输入：n = 1

输出："1"

解释：

这是基本情况。

提示：

1 <= n <= 30

进阶：你能迭代解决该问题吗？

Code

240907

解法：通过递归解决。

class Solution {
public:
    string process(string origin){
        string result="";
        int cur1=0, cur2=0;
        int size=origin.size();
        while(cur1<size && cur2<size){
            while(cur2<size && origin[cur1]==origin[cur2]) cur2++;
            result+=to_string(cur2-cur1);
            result+=origin[cur1];
            cur1=cur2;
        }
        return result;
    }
    string countAndSay(int n) {
        if(n==1) return "1";
        string res=countAndSay(n-1);
        return process(res);
    }
};

39. 组合总和

中等

给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的所有 不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合。

candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。

对于给定的输入，保证和为 target 的不同组合数少于 150 个。

示例 1：

输入：candidates = [2,3,6,7], target = 7
输出：[[2,2,3],[7]]
解释：
2 和 3 可以形成一组候选，2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选， 7 = 7 。
仅有这两种组合。

示例 2：

输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]

示例 3：

输入: candidates = [2], target = 1
输出: []

提示：

1 <= candidates.length <= 30
2 <= candidates[i] <= 40
candidates 的所有元素 互不相同
1 <= target <= 40

Code

240908

经典的DP，但是下面的代码还没有优化为一维的。

class Solution {
public:
    // int dp[50][50];
    vector<vector<int>> dp[50][50];
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        sort(candidates.begin(),candidates.end());
        int size=candidates.size();
        // dp[0][0].emplace_back(vector<int>{});
        for(int j=0;j<=target;j++){
            if(j%candidates[0]==0){
                vector<int> temp;
                for(int k=0;k<j/candidates[0];k++){
                    temp.emplace_back(candidates[0]);
                }
                dp[0][j].emplace_back(temp);
            }
        }
        for(int i=1;i<size;i++){
            int candidate=candidates[i];
            for(int j=0;j<=target;j++){
                dp[i][j]=dp[i-1][j];
            }
            for(int j=candidate;j<=target;j++){
                for(auto& k:dp[i][j-candidate]){
                    vector<int> temp=k;
                    temp.emplace_back(candidate);
                    dp[i][j].emplace_back(temp);
                }
            }
        }
        return dp[size-1][target];
        // sort(candidates.begin(),candidates.end());
        // int size=candidates.size();
        // memset(dp,0,sizeof(dp));
        // dp[0][0]=1;
        // for(int j=1;j<target;j++){
        //     if(j/candidates[0]) dp[0][j]=0;
        //     else dp[0][j]=1;
        // }
        // for(int i=1;i<size;i++){
        //     int candidate=candidates[i];
        //     for(int j=0;j<candidate;j++){
        //         dp[i][j]=dp[i-1][j];
        //     }
        //     for(int j=candidate;j<target;j++){
        //         dp[i][j]=dp[i-1][j]+dp[i][j-candidate];
        //     }
        // }
        // return dp[size-1][target];
    }
};

40. 组合总和 II

中等

给定一个候选人编号的集合 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用一次。

注意：解集不能包含重复的组合。

示例 1:

输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]

示例 2:

输入: candidates = [2,5,2,1,2], target = 5,
输出:
[
[1,2,2],
[5]
]

提示:

1 <= candidates.length <= 100
1 <= candidates[i] <= 50
1 <= target <= 30

Code1

240909

没有去重的写法，答案错误。但是是一维DP

class Solution {
public:
    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
        sort(candidates.begin(),candidates.end());
        int size=candidates.size();
        vector<vector<int>> dp[50];
        dp[0].emplace_back(vector<int>{});
        for(int i=0;i<size;i++){
            for(int j=target;j>=candidates[i];j--){
                for(auto k:dp[j-candidates[i]]){
                    k.emplace_back(candidates[i]);
                    dp[j].emplace_back(k);
                }
            }
        }
        return dp[target];
        //没有去重
    }
};

Code2

2409090

时间优化不够，因为是set

class Solution {
public:
    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
        sort(candidates.begin(),candidates.end());
        int size=candidates.size();
        set<vector<int>> dp[50];
        dp[0].insert(vector<int>{});
        for(int i=0;i<size;i++){
            for(int j=target;j>=candidates[i];j--){
                for(auto k:dp[j-candidates[i]]){
                    k.emplace_back(candidates[i]);
                    dp[j].insert(k);
                }
            }
        }
        return vector<vector<int>> (dp[target].begin(),dp[target].end());
        //用set去重
    }
};

43. 字符串相乘

中等

给定两个以字符串形式表示的非负整数 num1 和 num2，返回 num1 和 num2 的乘积，它们的乘积也表示为字符串形式。

注意：不能使用任何内置的 BigInteger 库或直接将输入转换为整数。

示例 1:

输入: num1 = "2", num2 = "3"
输出: "6"

示例 2:

输入: num1 = "123", num2 = "456"
输出: "56088"

提示：

1 <= num1.length, num2.length <= 200
num1 和 num2 只能由数字组成。
num1 和 num2 都不包含任何前导零，除了数字0本身。

Code

240911

class Solution {
public:
    string plus(string num1, string num2){
        string result="";
        int len1=num1.length();
        int len2=num2.length();
        int temp=0;
        int cur1=len1-1;
        int cur2=len2-1;
        while(cur1>=0 && cur2>=0){
            temp+=num1[cur1]-'0'+num2[cur2]-'0';
            result=to_string(temp%10)+result;
            temp/=10;
            cur1--;cur2--;
        }
        while(cur1>=0){
            temp+=num1[cur1]-'0';
            result=to_string(temp%10)+result;
            temp/=10;
            cur1--;
        }
        while(cur2>=0){
            temp+=num2[cur2]-'0';
            result=to_string(temp%10)+result;
            temp/=10;
            cur2--;
        }
        if(temp){
            result=to_string(temp)+result;
        }
        return result;
    }
    string multi(string num1, char num2, int digits){
        string result="";
        int cur1=num1.length()-1;
        int num3=num2-'0';
        int temp=0;
        while(cur1>=0){
            temp+=(num1[cur1]-'0')*num3;
            result=to_string(temp%10)+result;
            temp/=10;
            cur1--;
        }
        while(temp){
            result=to_string(temp%10)+result;
            temp/=10;
        }
        while(digits--){
            result+="0";
        }
        return result;
    }
    string multiply(string num1, string num2) {
        string result="0";
        int len1=num1.length(), len2=num2.length();
        for(int i=len2-1;i>=0;i--){
            string temp1=multi(num1, num2[i], len2-1-i);
            result=plus(result, temp1);
        }
        int cur=0;
        while(cur<result.length()-1 && result[cur]=='0') cur++;
        result.erase(0,cur);
        return result;
    }
};

45. 跳跃游戏 II

中等

给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。

每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说，如果你在 nums[i] 处，你可以跳转到任意 nums[i + j] 处:

0 <= j <= nums[i]
i + j < n

返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。

示例 1:

输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
     从下标为 0 跳到下标为 1 的位置，跳 1 步，然后跳 3 步到达数组的最后一个位置。

示例 2:

输入: nums = [2,3,0,1,4]
输出: 2

提示:

1 <= nums.length <= 104
0 <= nums[i] <= 1000
题目保证可以到达 nums[n-1]

Code1

240912

简单题，直接遍历一遍即可？

class Solution {
public:
    int jump(vector<int>& nums) {
        int size=nums.size();
        int dp[size];
        memset(dp,0,sizeof(dp));
        for(int i=0;i<size;i++){
            int begin=i+1;
            int end=min(size-1,i+nums[i]);
            for(int j=begin;j<=end;j++){
                if(dp[j]==0) dp[j]=dp[i]+1;
                else dp[j]=min(dp[j],dp[i]+1);
            }
            // for(int k=0;k<size;k++) cout<<dp[k]<<" ";
            // cout<<endl;
        }
        return dp[size-1];
    }
};

Code2

240912

优化，每一跳计算能到的最小点和最大点。由于这个范围能覆盖(min,max)这个区间，所以只要最后一个点落在这个区间内，循环就结束。

class Solution {
public:
    int jump(vector<int>& nums) {
        int size=nums.size();
        int begin=0;
        int end=1;
        int res=0;
        while(end<size){
            int maxPos=0;
            for(int i=begin;i<end;i++){
                maxPos=max(maxPos,nums[i]+i);
            }
            begin=end;
            end=maxPos+1;
            res++;
        }
        return res;
    }
};

46. 全排列

中等

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

示例 2：

输入：nums = [0,1]
输出：[[0,1],[1,0]]

示例 3：

输入：nums = [1]
输出：[[1]]

提示：

1 <= nums.length <= 6
-10 <= nums[i] <= 10
nums 中的所有整数 互不相同

Code1

240912

看完题解后非常愚蠢的做法。

class Solution {
public:
    vector<vector<int>> Insert(vector<int>& nums, int target){
        vector<vector<int>> result;
        for(int i=0;i<=nums.size();i++){
            vector<int> temp=nums;
            temp.insert(temp.begin()+i,target);
            result.emplace_back(temp);
        }
        return result;
    }
    vector<vector<int>> permute(vector<int>& nums) {
        vector<vector<int>> result={vector<int>{}};
        for(int i=0;i<nums.size();i++){
            vector<vector<int>> temp;
            for(auto& vec:result){
                vector<vector<int>> temp2=Insert(vec,nums[i]);
                temp.insert(temp.end(),temp2.begin(),temp2.end());
            }
            result=temp;
        }
        return result;
    }
};

47. 全排列 II

中等

给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

示例 1：

输入：nums = [1,1,2]
输出：
[[1,1,2],
 [1,2,1],
 [2,1,1]]

示例 2：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

提示：

1 <= nums.length <= 8
-10 <= nums[i] <= 10

Code

240917

看了一部分题解自己又做了一点。

感觉被前面那题的思维限制住了。

class Solution {
public:
    void solve(vector<int>& now, vector<vector<int>>& res, vector<int>& nums, vector<int>& vis){
        if(now.size()==nums.size()){
            res.emplace_back(now);
            return;
        }
        for(int i=0;i<nums.size();i++){
            if(vis[i] || (i>0 && nums[i]==nums[i-1] && !vis[i-1]))
                continue;
            vis[i]=1;
            now.emplace_back(nums[i]);
            solve(now, res, nums, vis);
            now.pop_back();
            vis[i]=0;
        }
    }
    vector<vector<int>> permuteUnique(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        vector<vector<int>> res;
        vector<int> now;
        vector<int> vis(nums.size(), 0);
        solve(now, res, nums, vis);
        return res;
    }
};

48. 旋转图像

中等

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在原地旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

示例 1：

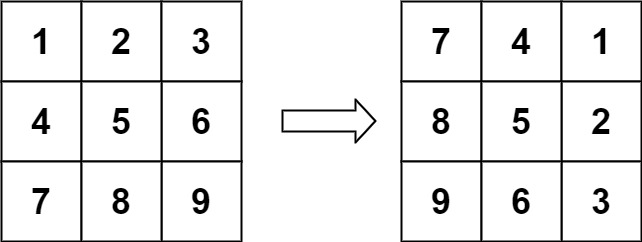
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]

示例 2：

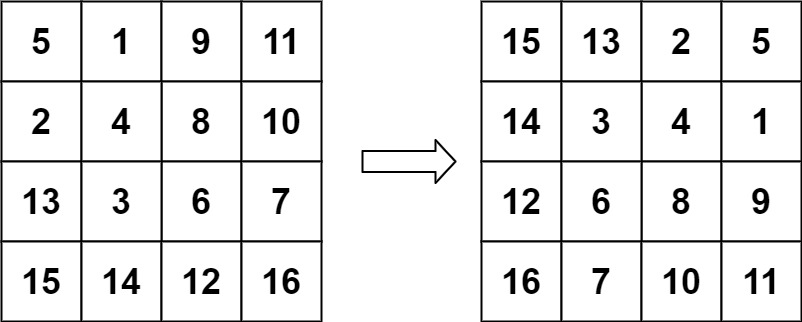
输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

提示：

n == matrix.length == matrix[i].length
1 <= n <= 20
-1000 <= matrix[i][j] <= 1000

Code

240918

class Solution {
public:
    vector<vector<int>> matrix_multiply(vector<vector<int>>& matrix1, vector<vector<int>>& matrix2){
        vector<vector<int>> res(matrix1.size(),vector<int>(matrix2[0].size(),0));
        for(int i=0;i<matrix1.size();i++){
            for(int j=0;j<matrix2[0].size();j++){
                int sum=0;
                for(int k=0;k<matrix2.size();k++){
                    sum+=matrix1[i][k]*matrix2[k][j];
                }
                res[i][j]=sum;
            }
        }
        return res;
    }
    void rotate_lap(vector<vector<int>>& matrix,int lap){
        int temp = matrix[lap][0];
        for(int i=lap+1;i<matrix.size()-lap;i++){
            swap(temp,matrix[lap][i]);
        }
        for(int j=lap+1;j<matrix.size()-lap;j++){
            swap(temp,matrix[j][matrix.size()-lap-1]);
        }
        for(int i=matrix.size()-lap-1;i>=0;i--){
            swap(temp,matrix[matrix.size()-lap-1][i]);
        }
        for(int j=matrix.size()-lap-1;j>=0;j--){
            swap(temp,matrix[j][lap]);
        }
    }
    void print(vector<vector<int>>& matrix){
        int size=matrix.size();
        for(int i=0;i<size;i++){
            for(int j=0;j<size;j++){
                cout<<matrix[i][j]<<" ";
            }
            cout<<endl;
        }
    }
    void rotate(vector<vector<int>>& matrix) {
        print(matrix);
        vector<vector<int>> mat(matrix.size(),vector<int>(matrix.size(),0));
        for(int i=0;i<matrix.size();i++){
            mat[i][matrix.size()-1-i]=1;
        }
        matrix = matrix_multiply(matrix,mat);
        for(int i=0;i<matrix.size();i++){
            for(int j=0;j<matrix.size()-i;j++){
                swap(matrix[i][j],matrix[matrix.size()-1-j][matrix.size()-1-i]);
            }
        }
        print(matrix);
    }
};

49. 字母异位词分组

中等

给你一个字符串数组，请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。

字母异位词 是由重新排列源单词的所有字母得到的一个新单词。

示例 1:

输入: strs = ["eat", "tea", "tan", "ate", "nat", "bat"]
输出: [["bat"],["nat","tan"],["ate","eat","tea"]]

示例 2:

输入: strs = [""]
输出: [[""]]

示例 3:

输入: strs = ["a"]
输出: [["a"]]

提示：

1 <= strs.length <= 104
0 <= strs[i].length <= 100
strs[i] 仅包含小写字母

Code1

240920

最基本的遍历。但是效率很低。需要优化

class Solution {
public:
    vector<int> decompose(string str){
        vector<int> res(26,0);
        for(auto& chr:str)
            res[chr-'a']++;
        return res;
    }
    bool compair(vector<int>& vec1,vector<int>& vec2){
        for(int i=0;i<26;i++)
            if(vec1[i]!=vec2[i]) return false;
        return true;
    }
    int check(vector<vector<int>>& res_digits, vector<int>& digits){
        for(int i=0;i<res_digits.size();i++)
            if(compair(res_digits[i],digits)) return i;
        return -1;
    }
    vector<vector<string>> groupAnagrams(vector<string>& strs) {
        vector<vector<string>> res;
        vector<vector<int>> res_digits;
        for(auto& str:strs){
            vector<int> digits = decompose(str);
            int find=check(res_digits,digits);
            if(find!=-1){
                res[find].emplace_back(str);
            }else{
                vector<string> temp;
                temp.emplace_back(str);
                res.emplace_back(temp);
                res_digits.emplace_back(digits);
            }
        }
        return res;
    }
};

Code2

240920

优化了一下，现在只要31ms了。上面的代码需要1s。

class Solution {
public:
    vector<vector<string>> groupAnagrams(vector<string>& strs) {
        unordered_map<string,vector<string>> umap;
        for(auto& str:strs){
            string sorted_str = str;
            sort(sorted_str.begin(), sorted_str.end());
            if(umap[sorted_str].size())
                umap[sorted_str].emplace_back(str);
            else
                umap[sorted_str]=vector<string> {str};
        }
        vector<vector<string>> res;
        for(auto& item:umap)
            res.emplace_back(item.second);
        return res;
    }
};

Code3

240920

现在21ms了，内存消耗22.18MB

class Solution {
public:
    vector<vector<string>> groupAnagrams(vector<string>& strs) {
        vector<vector<string>> res;
        unordered_map<string,int> umap;
        for(auto& str:strs){
            string sorted_str = str;
            sort(sorted_str.begin(), sorted_str.end());
            if(umap.find(sorted_str)!=umap.end())
                res[umap[sorted_str]].emplace_back(str);
            else{
                umap[sorted_str]=res.size();
                res.emplace_back(vector<string>{str});
            }
        }
        return res;
    }
};

50. Pow(x, n)

中等

实现 pow(x, n) ，即计算 x 的整数 n 次幂函数（即，xn ）。

示例 1：

输入：x = 2.00000, n = 10
输出：1024.00000

示例 2：

输入：x = 2.10000, n = 3
输出：9.26100

示例 3：

输入：x = 2.00000, n = -2
输出：0.25000
解释：2-2 = 1/22 = 1/4 = 0.25

提示：

-100.0 < x < 100.0
-231 <= n <= 231-1
n 是一个整数
要么 x 不为零，要么 n > 0 。
-104 <= xn <= 104

Code

240921

快速幂

class Solution {
public:
    double PoOoW(double x, long long n){
        double ans = 1.0;
        double temp = x;
        while(n){
            if(n&1) ans *= temp;
            temp *= temp;
            n >>= 1;
        }
        return ans;
    }
    double myPow(double x, int n){
        if(n>=0) return PoOoW(x, n);
        else return 1/PoOoW(x, -(long long)n);
        //写错了，并且还有一点错误
        // if(x>1){
        //     double up=x, down=1, mid;
        //     while(up-down>0.000005){
        //         mid=(up+down)/2;
        //         if(PoOoW(mid, -n)>x) up=mid;
        //         else down=mid;
        //     }
        //     return up;
        // }else if(x>0){
        //     double up=1, down=x, mid;
        //     while(up-down>0.000005){
        //         mid=(up+down)/2;
        //         if(PoOoW(mid, n)>x) up=mid;
        //         else down=mid;
        //     }
        //     return up;
        // }else if(x>-1){
        //     double up=x, down=-1, mid;
        //     while(up-down>0.000005){
        //         mid=(up+down)/2;
        //         if(PoOoW(mid, n)>x) up=mid;
        //         else down=mid;
        //     }
        //     return up;
        // }else{
        //     double up=-1, down=x, mid;
        //     while(up-down>0.000005){
        //         mid=(up+down)/2;
        //         if(PoOoW(mid, n)>x) up=mid;
        //         else down=mid;
        //     }
        //     return up;
        // }
    }
};

53. 最大子数组和

中等

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组

是数组中的一个连续部分。

示例 1：

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

示例 2：

输入：nums = [1]
输出：1

示例 3：

输入：nums = [5,4,-1,7,8]
输出：23

提示：

1 <= nums.length <= 105
-104 <= nums[i] <= 104

进阶：如果你已经实现复杂度为 O(n) 的解法，尝试使用更为精妙的 分治法 求解。

Code

240922

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int Max = INT_MIN;
        int sum = 0;
        for(auto& num:nums){
            sum=max(sum+num,num);
            Max=max(sum,Max);
        }
        return Max;
    }
};

54. 螺旋矩阵

中等

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

示例 1：

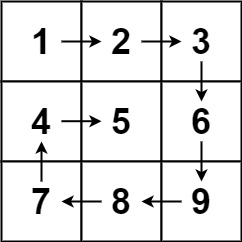
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

示例 2：

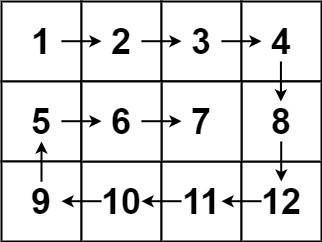
输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出：[1,2,3,4,8,12,11,10,9,5,6,7]

提示：

m == matrix.length
n == matrix[i].length
1 <= m, n <= 10
-100 <= matrix[i][j] <= 100

Code

240923

class Solution {
public:
    vector<int> spiralOrder(vector<vector<int>>& matrix) {
        vector<int> res;
        int row_start=0;
        int row_end=matrix.size()-1;
        int col_start=0;
        int col_end=matrix[0].size()-1;
        while(row_start<=row_end && col_start<=col_end){
            for(int i=col_start;i<=col_end;i++)
                res.emplace_back(matrix[row_start][i]);
            row_start++;
            for(int i=row_start;i<=row_end;i++)
                res.emplace_back(matrix[i][col_end]);
            col_end--;
            if(row_start>row_end) break;
            for(int i=col_end;i>=col_start;i--)
                res.emplace_back(matrix[row_end][i]);
            row_end--;
            if(col_start>col_end) break;
            for(int i=row_end;i>=row_start;i--)
                res.emplace_back(matrix[i][col_start]);
            col_start++;
        }
        cout<<row_start<<" "<<row_end<<" "<<col_start<<" "<<col_end<<endl;
        return res;
    }
};

55. 跳跃游戏

中等

给你一个非负整数数组 nums ，你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个下标，如果可以，返回 true ；否则，返回 false 。

示例 1：

输入：nums = [2,3,1,1,4]
输出：true
解释：可以先跳 1 步，从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。

示例 2：

输入：nums = [3,2,1,0,4]
输出：false
解释：无论怎样，总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 ， 所以永远不可能到达最后一个下标。

提示：

1 <= nums.length <= 104
0 <= nums[i] <= 105

Code

240924

class Solution {
public:
    bool canJump(vector<int>& nums) {
        int size=nums.size();
        if(size==1) return true;
        int start=0,end=1;
        while(start<end){
            int Max=end-1;
            for(int i=start;i<end;i++){
                Max=max(Max,i+nums[i]);
            }
            if(Max<end) return false;
            // cout<<start<<" "<<end<<" "<<Max<<endl;
            start=end;
            end=Max+1;
            if(end>=size) return true;
        }
        return true;
    }
};

56. 合并区间

中等

以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间，并返回 一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间 。

示例 1：

输入：intervals = [[1,3],[2,6],[8,10],[15,18]]
输出：[[1,6],[8,10],[15,18]]
解释：区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].

示例 2：

输入：intervals = [[1,4],[4,5]]
输出：[[1,5]]
解释：区间 [1,4] 和 [4,5] 可被视为重叠区间。

提示：

1 <= intervals.length <= 104
intervals[i].length == 2
0 <= starti <= endi <= 104

Code

240925

只能说速度非常慢。因为是O(n)的遍历。

class Solution {
public:
    vector<vector<int>> merge(vector<vector<int>>& intervals) {
        // int size=intervals.size();
        // int temp_array[size*2];
        // for(int i=0;i<size;i++){
        //     temp_array[i*2]=intervals[i][0];
        //     temp_array[i*2+1]=intervals[i][1];
        // }
        vector<vector<int>> res;
        sort(intervals.begin(),intervals.end(),[&](const vector<int>& a,const vector<int>& b){
            if(a[0]==b[0]) return a[1]>b[1];
            return a[0]<b[0];
        });
        // for(auto& interval:intervals) cout<<interval[0]<<" "<<interval[1]<<endl;
        int size=intervals.size();
        int cur=0;
        while(cur<size){
            int begin=intervals[cur][0];
            int Max=intervals[cur][1];
            while(cur<size && intervals[cur][0]<=Max){
                Max=max(Max,intervals[cur][1]);
                cur++;
            }
            res.emplace_back(vector<int>{begin,Max});
        }
        return res;
    }
};

很神奇的是，如果我把begin和Max的定义放在外面：

就会超时。不知道什么原因。

class Solution {
public:
    vector<vector<int>> merge(vector<vector<int>>& intervals) {
        vector<vector<int>> res;
        int size=intervals.size();
        sort(intervals.begin(),intervals.end(),[&](const vector<int>& a,const vector<int>& b){
            if(a[0]==b[0]) return a[1]>b[1];
            return a[0]<b[0];
        });
        int cur=0;
        int begin=intervals[cur][0];
        int end=intervals[cur][1];
        while(cur<size){
            // int begin=intervals[cur][0];
            // int end=intervals[cur][1];
            while(cur<size && intervals[cur][0]<=end){
                end=max(end,intervals[cur][1]);
                cur++;
            }
            res.emplace_back(vector<int>{begin,end});
        }
        return res;
    }
};

本来还想使用对分搜索优化，但是后面发现无论如何都需要排序，且扫描必须使用线性的。上面的解答的时间已经最优化了。

57. 插入区间

中等

给你一个 无重叠的 ，按照区间起始端点排序的区间列表 intervals，其中 intervals[i] = [starti, endi] 表示第 i 个区间的开始和结束，并且 intervals 按照 starti 升序排列。同样给定一个区间 newInterval = [start, end] 表示另一个区间的开始和结束。

在 intervals 中插入区间 newInterval，使得 intervals 依然按照 starti 升序排列，且区间之间不重叠（如果有必要的话，可以合并区间）。

返回插入之后的 intervals。

注意你不需要原地修改 intervals。你可以创建一个新数组然后返回它。

示例 1：

输入：intervals = [[1,3],[6,9]], newInterval = [2,5]
输出：[[1,5],[6,9]]

示例 2：

输入：intervals = [[1,2],[3,5],[6,7],[8,10],[12,16]], newInterval = [4,8]
输出：[[1,2],[3,10],[12,16]]
解释：这是因为新的区间 [4,8] 与 [3,5],[6,7],[8,10] 重叠。

提示：

0 <= intervals.length <= 104
intervals[i].length == 2
0 <= starti <= endi <= 105
intervals 根据 starti 按升序排列
newInterval.length == 2
0 <= start <= end <= 105

Code

240926

class Solution {
public:
    vector<vector<int>> insert(vector<vector<int>>& intervals, vector<int>& newInterval) {
        if(intervals.size()==0) return vector<vector<int>>{newInterval};
        int size=intervals.size();
        int start=0;
        while(start<size){
            if(intervals[start][1]>=newInterval[0]) break;
            start++;
        }
        int end=start;
        while(end<size){
            if(intervals[end][0]>newInterval[1]) break;
            end++;
        }
        cout<<start<<" "<<end<<endl;
        if(start==size){
            intervals.emplace_back(newInterval);
            return intervals;
        }else if(end==0){
            intervals.insert(intervals.begin(),newInterval);
            return intervals;
        }
        vector<int> New={min(intervals[start][0],newInterval[0]),max(intervals[end-1][1],newInterval[1])};
        intervals.erase(intervals.begin()+start,intervals.begin()+end);
        intervals.insert(intervals.begin()+start,New);
        return intervals;
    }
};

class Solution {
public:
    vector<vector<int>> insert(vector<vector<int>>& intervals, vector<int>& newInterval) {
        if(intervals.size()==0)
            return vector<vector<int>>{newInterval};
        int size=intervals.size();
        int start=0;
        while(start<size){
            if(intervals[start][1]>=newInterval[0]) break;
            start++;
        }
        int end=start;
        while(end<size){
            if(intervals[end][0]>newInterval[1]) break;
            end++;
        }
        if(start==size)
            intervals.emplace_back(newInterval);
        else if(end==0)
            intervals.insert(intervals.begin(),newInterval);
        else{
            vector<int> res={min(intervals[start][0],newInterval[0]),max(intervals[end-1][1],newInterval[1])};
            intervals.erase(intervals.begin()+start,intervals.begin()+end);
            intervals.insert(intervals.begin()+start,res);
        }
        return intervals;
    }
};

58. 最后一个单词的长度

简单

给你一个字符串 s，由若干单词组成，单词前后用一些空格字符隔开。返回字符串中 最后一个 单词的长度。

单词是指仅由字母组成、不包含任何空格字符的最大子字符串。

示例 1：

输入：s = "Hello World"
输出：5
解释：最后一个单词是“World”，长度为 5。

示例 2：

输入：s = "   fly me   to   the moon  "
输出：4
解释：最后一个单词是“moon”，长度为 4。

示例 3：

输入：s = "luffy is still joyboy"
输出：6
解释：最后一个单词是长度为 6 的“joyboy”。

提示：

1 <= s.length <= 104
s 仅有英文字母和空格 ' ' 组成
s 中至少存在一个单词

Code

240927

class Solution {
public:
    int lengthOfLastWord(string s) {
        int size=s.length();
        int end=size-1;
        while(end>=0 && s[end]==' ') end--;
        int start=end;
        while(start>=0 && s[start]!=' ') start--;
        return end-start;
    }
};

59. 螺旋矩阵 II

中等

给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

示例 1：

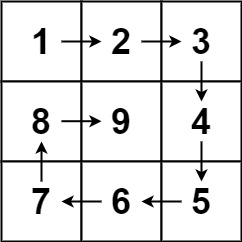
输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]

示例 2：

输入：n = 1
输出：[[1]]

提示：

1 <= n <= 20

Code

240927

class Solution {
public:
    vector<vector<int>> generateMatrix(int n) {
        vector<vector<int>> res(n,vector<int>(n));
        int row_start=0,row_end=n-1;
        int col_start=0,col_end=n-1;
        int i,now=1;
        while(row_start<=row_end && col_start<=col_end){
            for(i=col_start;i<=col_end;i++)
                res[row_start][i]=now++;
            row_start++;
            for(i=row_start;i<=row_end;i++)
                res[i][col_end]=now++;
            col_end--;
            for(i=col_end;i>=col_start;i--)
                res[row_end][i]=now++;
            row_end--;
            for(i=row_end;i>=row_start;i--)
                res[i][col_start]=now++;
            col_start++;
        }
        return res;
    }
};

61. 旋转链表

中等

给你一个链表的头节点 head ，旋转链表，将链表每个节点向右移动 k 个位置。

示例 1：

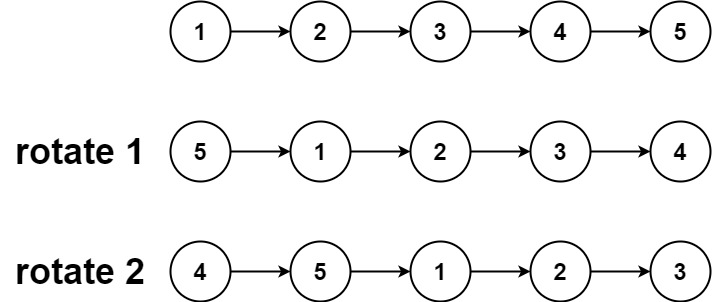
输入：head = [1,2,3,4,5], k = 2
输出：[4,5,1,2,3]

示例 2：

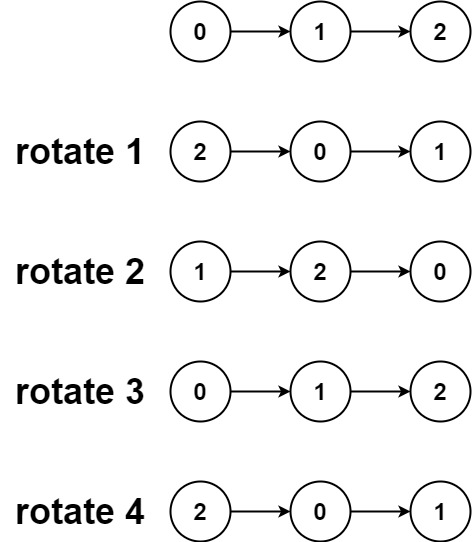
输入：head = [0,1,2], k = 4
输出：[2,0,1]

提示：

链表中节点的数目在范围 [0, 500] 内
-100 <= Node.val <= 100
0 <= k <= 2 * 109

Code

240929

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* rotate(ListNode* head){
        ListNode* p=head;
        while(p->next->next!=nullptr) p=p->next;
        ListNode* old_head=head;
        head=p->next;
        p->next=nullptr;
        head->next=old_head;
        return head;
    }
    ListNode* rotateRight(ListNode* head, int k) {
        int len=0;
        ListNode* temp_head=head;
        while(temp_head!=nullptr){
            len++;
            temp_head=temp_head->next;
        }
        if(len==0) return nullptr;
        if(len==1) return head;
        // if(k) k++;
        k=k%len;
        while(k--) head=rotate(head);
        return head;
    }
};

62. 不同路径

中等

一个机器人位于一个 m x n 网格的左上角（起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

示例 1：

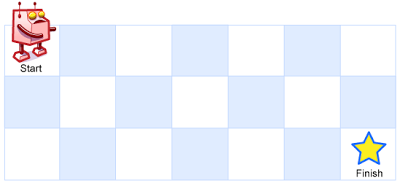
输入：m = 3, n = 7
输出：28

示例 2：

输入：m = 3, n = 2
输出：3
解释：
从左上角开始，总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下

示例 3：

输入：m = 7, n = 3
输出：28

示例 4：

输入：m = 3, n = 3
输出：6

提示：

1 <= m, n <= 100
题目数据保证答案小于等于 2 * 109

Code

240929

class Solution {
public:
    int uniquePaths(int m, int n) {
        int paths[m];
        memset(paths,0,sizeof(paths));
        // for(int i=0;i<m;i++) paths[i]=i;
        paths[0]=1;
        for(int i=0;i<n;i++)
            for(int j=1;j<m;j++) paths[j]+=paths[j-1];
        return paths[m-1];
    }
};

63. 不同路径 II

中等

给定一个 m x n 的整数数组 grid。一个机器人初始位于 左上角（即 grid[0][0]）。机器人尝试移动到 右下角（即 grid[m - 1][n - 1]）。机器人每次只能向下或者向右移动一步。

网格中的障碍物和空位置分别用 1 和 0 来表示。机器人的移动路径中不能包含任何有障碍物的方格。

返回机器人能够到达右下角的不同路径数量。

测试用例保证答案小于等于 2 * 109。

示例 1：

输入：obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出：2
解释：3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右

示例 2：

输入：obstacleGrid = [[0,1],[0,0]]
输出：1

提示：

m == obstacleGrid.length
n == obstacleGrid[i].length
1 <= m, n <= 100
obstacleGrid[i][j] 为 0 或 1

Code

240929

class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        if(obstacleGrid[0][0]==1) return 0;
        int n=obstacleGrid.size();
        int m=obstacleGrid[0].size();
        vector<int> vec1(m,0),vec2(m,0);
        vec1[0]=1;
        for(int j=1;j<m;j++)
            if(obstacleGrid[0][j]==0) vec1[j]=vec1[j-1];
        for(int i=1;i<n;i++){
            if(obstacleGrid[i][0]==0) vec2[0]=vec1[0];
            else vec2[0]=0;
            for(int j=1;j<m;j++)
                if(obstacleGrid[i][j]==0) vec2[j]=vec2[j-1]+vec1[j];
                else vec2[j]=0;
            swap(vec1,vec2);
        }
        return vec1[m-1];
    }
};

71. 简化路径

中等

给你一个字符串 path ，表示指向某一文件或目录的 Unix 风格 绝对路径 （以 '/' 开头），请你将其转化为 更加简洁的规范路径。

在 Unix 风格的文件系统中规则如下：

一个点 '.' 表示当前目录本身。
此外，两个点 '..' 表示将目录切换到上一级（指向父目录）。
任意多个连续的斜杠（即，'//' 或 '///'）都被视为单个斜杠 '/'。
任何其他格式的点（例如，'...' 或 '....'）均被视为有效的文件/目录名称。

返回的 简化路径 必须遵循下述格式：

始终以斜杠 '/' 开头。
两个目录名之间必须只有一个斜杠 '/' 。
最后一个目录名（如果存在）不能以 '/' 结尾。
此外，路径仅包含从根目录到目标文件或目录的路径上的目录（即，不含 '.' 或 '..'）。

返回简化后得到的 规范路径 。

示例 1：

输入：path = "/home/"

输出："/home"

解释：

应删除尾随斜杠。

示例 2：

输入：path = "/home//foo/"

输出："/home/foo"

解释：

多个连续的斜杠被单个斜杠替换。

示例 3：

输入：path = "/home/user/Documents/../Pictures"

输出："/home/user/Pictures"

解释：

两个点 ".." 表示上一级目录（父目录）。

示例 4：

输入：path = "/../"

输出："/"

解释：

示例 5：

输入：path = "/.../a/../b/c/../d/./"

输出："/.../b/d"

解释：

"..." 在这个问题中是一个合法的目录名。

提示：

1 <= path.length <= 3000
path 由英文字母，数字，'.'，'/' 或 '_' 组成。
path 是一个有效的 Unix 风格绝对路径。

Code

241007

class Solution {
public:
    string simplifyPath(string path) {
        vector<string> paths;
        int len=path.length();
        int cur=0;
        path+="/";
        while(cur<len){
            size_t next_slash=path.find('/',cur+1);
            if(next_slash==string::npos) break;
            string sub_path=path.substr(cur,next_slash-cur);
            cur=next_slash;
            // cout<<sub_path<<endl;
            if(sub_path=="/") continue;
            if(sub_path=="/.") continue;
            if(sub_path=="/.."){
                if(paths.size()) paths.pop_back();
                continue;
            }
            paths.emplace_back(sub_path);
        }
        string result="";
        for(auto& p:paths) result+=p;
        if(result=="") result="/";
        return result;
    }
};

73. 矩阵置零

中等

给定一个 *m* x *n* 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用原地算法。

示例 1：

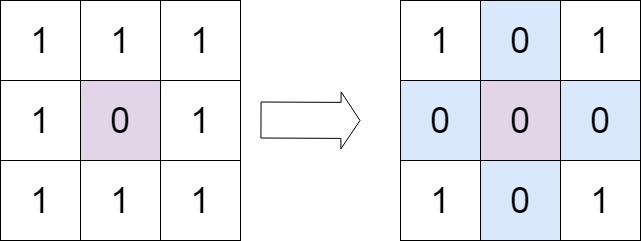
输入：matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出：[[1,0,1],[0,0,0],[1,0,1]]

示例 2：

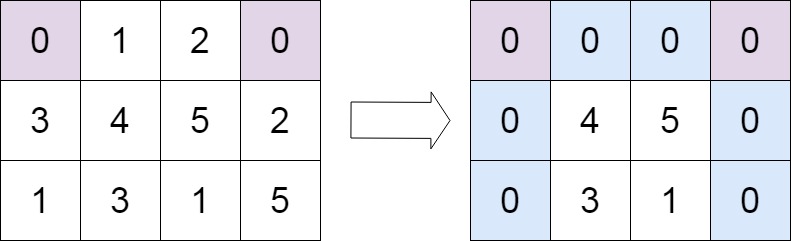
输入：matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出：[[0,0,0,0],[0,4,5,0],[0,3,1,0]]

提示：

m == matrix.length
n == matrix[0].length
1 <= m, n <= 200
-231 <= matrix[i][j] <= 231 - 1

进阶：

一个直观的解决方案是使用 O(*m**n*) 的额外空间，但这并不是一个好的解决方案。
一个简单的改进方案是使用 O(*m* + *n*) 的额外空间，但这仍然不是最好的解决方案。
你能想出一个仅使用常量空间的解决方案吗？

Code

241009

class Solution {
public:
    void setZeroes(vector<vector<int>>& matrix) {
        int first_col_has_0=0;
        int first_row_has_0=0;
        int m=matrix.size();
        int n=matrix[0].size();
        for(int i=0;i<m;i++){
            if(matrix[i][0]==0){
                first_row_has_0=1;
                break;
            }
        }
        for(int j=0;j<n;j++){
            if(matrix[0][j]==0){
                first_col_has_0=1;
                break;
            }
        }
        for(int i=1;i<m;i++){
            for(int j=1;j<n;j++){
                if(matrix[i][j]==0){
                    matrix[i][0]=0;
                    matrix[0][j]=0;
                }
            }
        }
        for(int i=1;i<m;i++){
            if(matrix[i][0]==0){
                for(int j=1;j<n;j++){
                    matrix[i][j]=0;
                }
            }
        }
        for(int j=1;j<n;j++){
            if(matrix[0][j]==0){
                for(int i=1;i<m;i++){
                    matrix[i][j]=0;
                }
            }
        }
        if(first_row_has_0){
            for(int i=0;i<m;i++){
                matrix[i][0]=0;
            }
        }
        if(first_col_has_0){
            for(int j=0;j<n;j++){
                matrix[0][j]=0;
            }
        }
    }
};

75. 颜色分类

中等

给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums ，原地对它们进行排序，使得相同颜色的元素相邻，并按照红色、白色、蓝色顺序排列。

我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。

必须在不使用库内置的 sort 函数的情况下解决这个问题。

示例 1：

输入：nums = [2,0,2,1,1,0]
输出：[0,0,1,1,2,2]

示例 2：

输入：nums = [2,0,1]
输出：[0,1,2]

提示：

n == nums.length
1 <= n <= 300
nums[i] 为 0、1 或 2

进阶：

你能想出一个仅使用常数空间的一趟扫描算法吗？

Code

241009

class Solution {
public:
    void sortColors(vector<int>& nums) {
        int counts[3]={0,0,0};
        for(int i=0;i<nums.size();i++)
            counts[nums[i]]++;
        int cur=0;
        for(int i=0;i<3;i++)
            while(counts[i]--)
                nums[cur++]=i;
    }
};

77. 组合

中等

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按 任何顺序 返回答案。

示例 1：

输入：n = 4, k = 2
输出：
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]

示例 2：

输入：n = 1, k = 1
输出：[[1]]

提示：

1 <= n <= 20
1 <= k <= n

Code

241015

简单的递归。效率还挺高，时间103ms，击败90.56%。

但是如果在recursion函数的end、k参数上使用引用，就会使时间到达249ms，击败8.62%。非常神奇。

class Solution {
public:
    void recursion(vector<vector<int>>& res, vector<int>& now, int begin, int end, int k){
        if(now.size()==k) res.emplace_back(now);
        for(int i=begin;i<=end;i++){
            now.emplace_back(i);
            recursion(res,now,i+1,end,k);
            now.pop_back();
        }
    }
    vector<vector<int>> combine(int n, int k) {
        vector<vector<int>> res;
        vector<int> now;
        recursion(res,now,1,n,k);
        return res;
    }
};

78. 子集

中等

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）

解集不能包含重复的子集。你可以按 任意顺序 返回解集。

示例 1：

输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

示例 2：

输入：nums = [0]
输出：[[],[0]]

提示：

1 <= nums.length <= 10
-10 <= nums[i] <= 10
nums 中的所有元素 互不相同

Code

241015

还是简单的递归。记得排序就好了。

class Solution {
public:
    void recursion(vector<vector<int>>& res,vector<int>& now,vector<int>& nums,int cur){
        res.emplace_back(now);
        for(int i=cur;i<nums.size();i++){
            if(!i || nums[i]!=nums[i-1]){
                now.emplace_back(nums[i]);
                recursion(res,now,nums,i+1);
                now.pop_back();
            }
        }
    }
    vector<vector<int>> subsets(vector<int>& nums) {
        sort(nums.begin(),nums.end());
        vector<vector<int>> res;
        vector<int> now;
        recursion(res,now,nums,0);
        return res;
    }
};

105. 从前序与中序遍历序列构造二叉树

中等

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:

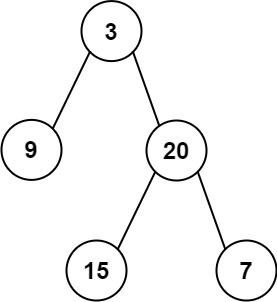
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

示例 2:

输入: preorder = [-1], inorder = [-1]
输出: [-1]

提示:

1 <= preorder.length <= 3000
inorder.length == preorder.length
-3000 <= preorder[i], inorder[i] <= 3000
preorder 和 inorder 均 无重复 元素
inorder 均出现在 preorder
preorder 保证为二叉树的前序遍历序列
inorder 保证为二叉树的中序遍历序列

Code

241106

76ms

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> subvec(vector<int> origin, int start, int end){
        return vector<int>(origin.begin() + start, origin.begin() + end);
    }
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        if(preorder.size()==0) return nullptr;
        int rootVal = preorder[0];
        int size = preorder.size();
        int cur = 0;
        while(inorder[cur]!=rootVal) cur++;
        TreeNode* now = new TreeNode(rootVal);
        vector<int> v1=subvec(preorder,1,cur+1);
        vector<int> v2=subvec(inorder,0,cur);
        vector<int> v3=subvec(preorder,cur+1,size);
        vector<int> v4=subvec(inorder,cur+1,size);
        now->left = buildTree(v1, v2);
        now->right = buildTree(v3, v4);
        return now;
    }
};

40ms

class Solution {
public:
    TreeNode* buildTree(vector<int> preorder, vector<int> inorder) {
        if(preorder.size()==0) return nullptr;
        int rootVal = preorder[0];
        int size = preorder.size();
        int cur = 0;
        while(inorder[cur]!=rootVal) cur++;
        TreeNode* now = new TreeNode(rootVal);
        now->left = buildTree(vector<int>(preorder.begin()+1,preorder.begin()+cur+1), vector<int>(inorder.begin()+0,inorder.begin()+cur));
        now->right = buildTree(vector<int>(preorder.begin()+cur+1, preorder.begin()+size), vector<int>(inorder.begin()+cur+1, inorder.begin()+size));
        return now;
    }
};

7ms 击败65.31%, 26.06MB 击败96.21%

class Solution {
public:
    TreeNode* myTree(vector<int>& preorder, vector<int>& inorder, int pre_left, int pre_right, int in_left, int in_right){
        if(pre_left == pre_right) return nullptr;
        int rootVal = preorder[pre_left];
        int cur = in_left;
        while(inorder[cur]!=rootVal) cur++;
        int offset = cur-in_left;
        TreeNode* now = new TreeNode(rootVal);
        now->left = myTree(preorder, inorder, pre_left+1, pre_left+offset+1, in_left, cur);
        now->right = myTree(preorder, inorder, pre_left+offset+1, pre_right, cur+1, in_right);
        return now;
    }
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        return myTree(preorder, inorder, 0, preorder.size(), 0, preorder.size());
    }
};

4ms | 击败73.74% , 26.29 MB | 击败70.29%

class Solution {
public:
    vector<int> preOrder, inOrder;
    TreeNode* myTree(int pre_left, int pre_right, int in_left, int in_right){
        if(pre_left == pre_right) return nullptr;
        int rootVal = preOrder[pre_left];
        int cur = in_left;
        while(inOrder[cur]!=rootVal) cur++;
        int offset = cur-in_left;
        TreeNode* now = new TreeNode(rootVal);
        now->left = myTree(pre_left+1, pre_left+offset+1, in_left, cur);
        now->right = myTree(pre_left+offset+1, pre_right, cur+1, in_right);
        return now;
    }
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        preOrder = preorder;
        inOrder = inorder;
        return myTree(0, preorder.size(), 0, preorder.size());
    }
};

179. 最大数

中等

给定一组非负整数 nums，重新排列每个数的顺序（每个数不可拆分）使之组成一个最大的整数。

注意：输出结果可能非常大，所以你需要返回一个字符串而不是整数。

示例 1：

输入：nums = [10,2]
输出："210"

示例 2：

输入：nums = [3,30,34,5,9]
输出："9534330"

提示：

1 <= nums.length <= 100
0 <= nums[i] <= 109

Code

240928

刚开始我想复杂了，其实直接两个不同顺序相加即可比较。

class Solution {
public:
    string largestNumber(vector<int>& nums) {
        int size=nums.size();
        string res="";
        vector<string> str(size);
        for(int i=0;i<size;i++){
            str[i]=to_string(nums[i]);
        }
        sort(str.begin(),str.end(),[&](const string& a,const string& b){
            return a+b>b+a;
            // if(a.length()==b.length()){
            //     for(int i=0;i<a.length();i++)
            //         if(a[i]!=b[i]) return a[i]>b[i];
            // }else{
            //     for(int i=0;i<min(a.length(),b.length());i++)
            //         if(a[i]!=b[i]) return a[i]>b[i];
            //     int cur_a=a.length()>b.length()?b.length():0;
            //     int cur_b=a.length()>b.length()?0:b.length();
            //     while(cur_a<a.length() && cur_b<b.length()){
            //         if(a[cur_a]!=b[cur_b]) return a[cur_a]>b[cur_b];
            //         cur_a++;
            //         cur_b++;
            //     }
            // }
            // return false;
        });
        for(auto& s:str) res+=s;
        auto it=res.begin();
        while(it!=res.end()-1 && *it=='0') it++;
        res.erase(res.begin(),it);
        return res;
    }
};

289. 生命游戏

中等

根据百度百科， 生命游戏 ，简称为生命，是英国数学家约翰·何顿·康威在 1970 年发明的细胞自动机。

给定一个包含 m × n 个格子的面板，每一个格子都可以看成是一个细胞。每个细胞都具有一个初始状态： 1 即为 活细胞 （live），或 0 即为 死细胞 （dead）。每个细胞与其八个相邻位置（水平，垂直，对角线）的细胞都遵循以下四条生存定律：

如果活细胞周围八个位置的活细胞数少于两个，则该位置活细胞死亡；
如果活细胞周围八个位置有两个或三个活细胞，则该位置活细胞仍然存活；
如果活细胞周围八个位置有超过三个活细胞，则该位置活细胞死亡；
如果死细胞周围正好有三个活细胞，则该位置死细胞复活；

下一个状态是通过将上述规则同时应用于当前状态下的每个细胞所形成的，其中细胞的出生和死亡是同时发生的。给你 m x n 网格面板 board 的当前状态，返回下一个状态。

示例 1：

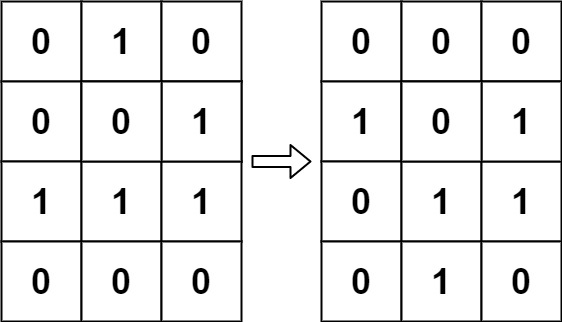
输入：board = [[0,1,0],[0,0,1],[1,1,1],[0,0,0]]
输出：[[0,0,0],[1,0,1],[0,1,1],[0,1,0]]

示例 2：

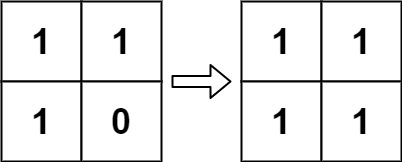
输入：board = [[1,1],[1,0]]
输出：[[1,1],[1,1]]

提示：

m == board.length
n == board[i].length
1 <= m, n <= 25
board[i][j] 为 0 或 1

进阶：

你可以使用原地算法解决本题吗？请注意，面板上所有格子需要同时被更新：你不能先更新某些格子，然后使用它们的更新后的值再更新其他格子。
本题中，我们使用二维数组来表示面板。原则上，面板是无限的，但当活细胞侵占了面板边界时会造成问题。你将如何解决这些问题？

Code

240927

class Solution {
public:
    int dx[9]={-1,-1,-1,0,0,1,1,1};
    int dy[9]={-1,0,1,-1,1,-1,0,1};
    int m,n;
    int calculate(vector<vector<int>>& board,int x,int y){
        int xx,yy,count=0;
        for(int i=0;i<8;i++){
            xx=x+dx[i];
            yy=y+dy[i];
            if(xx>=0 && xx<this->n && yy>=0 && yy<this->m)
                count+=board[xx][yy];
        }
        return count;
    }
    void gameOfLife(vector<vector<int>>& board) {
        this->n=board.size();
        this->m=board[0].size();
        vector<vector<int>> res=board;
        for(int i=0;i<this->n;i++){
            for(int j=0;j<this->m;j++){
                int result=calculate(board,i,j);
                // cout<<result<<" ";
                if(board[i][j]){
                    if(result<2) res[i][j]=0;
                    else if(result<=3) res[i][j]=1;
                    else res[i][j]=0;
                }else if(result==3) res[i][j]=1;
            }
            // cout<<endl;
        }
        board=res;
    }
};

LeetCode Notes

https://acm.nanyan.cc/posts/7582.html

作者

nanyan

发布于

2024年7月27日

许可协议

Hello World 上一篇

Advanced Algebra 下一篇