Codeforces Round

Round 923 (Div. 3)

240206

A. Make it White

time limit per test2 seconds memory limit per test256 megabytes inputstandard input outputstandard output

You have a horizontal strip of \(n\) cells. Each cell is either white or black.

You can choose a continuous segment of cells once and paint them all white. After this action, all the black cells in this segment will become white, and the white ones will remain white.

What is the minimum length of the segment that needs to be painted white in order for all \(n\) cells to become white?

Input

The first line of the input contains a single integer \(t(1≤𝑡≤10^4)\) — the number of test cases. The descriptions of the test cases follow.

The first line of each test case contains a single integer \(𝑛(1≤𝑛≤10)\) — the length of the strip.

The second line of each test case contains a string \(𝑠\), consisting of \(𝑛\) characters, each of which is either 'W' or 'B'. The symbol 'W' denotes a white cell, and 'B' — a black one. It is guaranteed that at least one cell of the given strip is black.

Output

For each test case, output a single number — the minimum length of a continuous segment of cells that needs to be painted white in order for the entire strip to become white.

Example

input

8
6
WBBWBW
1
B
2
WB
3
BBW
4
BWWB
6
BWBWWB
6
WWBBWB
9
WBWBWWWBW

output

4
1
1
2
4
6
4
7

Note

In the first test case of the example for the strip "WBBWBW", the minimum length of the segment to be repainted white is 4. It is necessary to repaint to white the segment from the 2-nd to the 5-th cell (the cells are numbered from 1 from left to right).

Code

#include<bits/stdc++.h>
using namespace std;
int main(){
    int c;
    cin>>c;
    while(c--){
        int len;
        cin>>len;
        string str;
        cin>>str;
        int begin=-1,end=-1;
        for(int i=0;i<len;i++){
            if(begin==-1 && str[i]=='B')    begin=i;
            if(str[i]=='B') end=i;
        }
        if(begin==-1 && end==-1){
            cout<<0<<endl;
        }else{
            cout<<end-begin+1<<endl;
        }
    }
    return 0;
}

B. Following the String

time limit per test2 seconds memory limit per test256 megabytes inputstandard input outputstandard output

Polycarp lost the string 𝑠 of length 𝑛 consisting of lowercase Latin letters, but he still has its trace.

The trace of the string 𝑠 is an array 𝑎 of 𝑛 integers, where 𝑎𝑖 is the number of such indices 𝑗 (𝑗<𝑖) that 𝑠𝑖=𝑠𝑗 . For example, the trace of the string abracadabra is the array [0,0,0,1,0,2,0,3,1,1,4].

Given a trace of a string, find any string 𝑠 from which it could have been obtained. The string 𝑠 should consist only of lowercase Latin letters a-z.

Input

The first line of the input contains a single integer 𝑡 (1≤𝑡≤104) — the number of test cases. Then the descriptions of the test cases follow.

The first line of each test case contains a single integer 𝑛 (1≤𝑛≤2⋅105) — the length of the lost string.

The second line of each test case contains 𝑛 integers 𝑎1,𝑎2,…,𝑎𝑛 (0≤𝑎𝑖<𝑛) — the trace of the string. It is guaranteed that for the given trace, there exists a suitable string 𝑠.

It is guaranteed that the sum of 𝑛 over all test cases does not exceed 2⋅105.

Output

For each test case, output a string 𝑠 that corresponds to the given trace. If there are multiple such strings 𝑠 , then output any of them.

The string 𝑠 should consist of lowercase Latin letters a-z.

It is guaranteed that for each test case, a valid answer exists.

Example

input

5
11
0 0 0 1 0 2 0 3 1 1 4
10
0 0 0 0 0 1 0 1 1 0
1
0
8
0 1 2 3 4 5 6 7
8
0 0 0 0 0 0 0 0

output

abracadabra
codeforces
a
aaaaaaaa
dijkstra

Code

#include<bits/stdc++.h>
using namespace std;
int main(){
    int c;
    cin>>c;
    while(c--){
        int n;
        cin>>n;
        vector<int> v(n);
        for(int i=0;i<n;i++){
            cin>>v[i];
        }
        map<char,int> m;
        for(char ch='a';ch<='z';ch++){
            m[ch]=0;
        }
        for(int i=0;i<n;i++){
            for(auto &k:m){
                if(k.second==v[i]){
                    cout<<k.first;
                    m[k.first]++;
                    break;
                }
            }
        }
        cout<<endl;
    }
    return 0;
}

C. Choose the Different Ones!

time limit per test2 seconds memory limit per test256 megabytes inputstandard input outputstandard output

Given an array 𝑎 of 𝑛 integers, an array 𝑏 of 𝑚 integers, and an even number 𝑘 .

Your task is to determine whether it is possible to choose exactly 𝑘2 elements from both arrays in such a way that among the chosen elements, every integer from 1 to 𝑘 is included.

For example:

If 𝑎=[2,3,8,5,6,5], 𝑏=[1,3,4,10,5], 𝑘=6, then it is possible to choose elements with values 2,3,6 from array 𝑎 and elements with values 1,4,5 from array 𝑏. In this case, all numbers from 1 to 𝑘=6 will be included among the chosen elements.

If 𝑎=[2,3,4,5,6,5], 𝑏=[1,3,8,10,3], 𝑘=6, then it is not possible to choose elements in the required way.

Note that you are not required to find a way to choose the elements — your program should only check whether it is possible to choose the elements in the required way.

Input

The first line of the input contains a single integer 𝑡(1≤𝑡≤104) — the number of test cases. The descriptions of the test cases follow.

The first line of each test case contains three integers 𝑛, 𝑚, and 𝑘(1≤𝑛,𝑚≤2⋅105, 2≤𝑘≤2⋅min(𝑛,𝑚), 𝑘 is even) — the length of array 𝑎, the length of array 𝑏, and the number of elements to be chosen, respectively.

The second line of each test case contains 𝑛 integers 𝑎1,𝑎2,…,𝑎𝑛(1≤𝑎𝑖≤10^6) — the elements of array 𝑎.

The third line of each test case contains 𝑚 integers 𝑏1,𝑏2,…,𝑏𝑚 (1≤𝑏𝑗≤10^6) — the elements of array 𝑏.

It is guaranteed that the sum of values 𝑛 and 𝑚 over all test cases in a test does not exceed 4⋅10^5.

Output

Output 𝑡 lines, each of which is the answer to the corresponding test case. As the answer, output "YES" if it is possible to choose 𝑘2 numbers from each array in such a way that among the chosen elements, every integer from 1 to 𝑘 is included. Otherwise, output "NO".

You can output each letter in any case (lowercase or uppercase). For example, the strings "yEs", "yes", "Yes", and "YES" will be accepted as a positive answer.

Example

input

6
6 5 6
2 3 8 5 6 5
1 3 4 10 5
6 5 6
2 3 4 5 6 5
1 3 8 10 3
3 3 4
1 3 5
2 4 6
2 5 4
1 4
7 3 4 4 2
1 4 2
2
6 4 4 2
1 5 2
3
2 2 1 4 3

output

YES
NO
YES
YES
NO
NO

Note

In the first test case of the example, it is possible to choose elements equal to 2, 3, and 6 from array 𝑎 and elements equal to 1, 4, and 5 from array 𝑏. Thus, all numbers from 1 to 𝑘=6 are included among the chosen elements.

In the second test case of the example, it can be shown that it is not possible to choose exactly three elements from each array in the required way.

In the third test case of the example, it is possible to choose elements equal to 1 and 3 from array 𝑎 and elements equal to 2 and 4 from array 𝑏. Thus, all numbers from 1 to 𝑘=4 are included among the chosen elements.

Code

#include<bits/stdc++.h>
using namespace std;
int main(){
    int t;
    cin>>t;
    while(t--){
        int n,m,k;
        cin>>n>>m>>k;
        vector<int> a(n),b(m);
        // vector<int> c(k+1,0);
        for(int i=0;i<n;i++)    cin>>a[i];
        for(int i=0;i<m;i++)    cin>>b[i];
        sort(a.begin(),a.end());
        sort(b.begin(),b.end());
        vector<int>::iterator cur_a,cur_b;
        // auto cur_a=upper_bound(a.begin(),a.end(),k);
        // if(cur_a!=a.end())  a.erase(cur_a);
        // auto cur_b=upper_bound(b.begin(),b.end(),k);
        // if(cur_b!=b.end())  b.erase(cur_b);
        int count_a=0,count_b=0,i;
        for(i=1;i<=k;i++){
            cur_a=lower_bound(a.begin(),a.end(),i);
            cur_b=lower_bound(b.begin(),b.end(),i);
            if(cur_a==a.end() && cur_b==b.end()){
                break;
            }else if(cur_a==a.end() && cur_b!=b.end()){
                if(*cur_b==i) count_b++;
                else break;
            }else if(cur_a!=a.end() && cur_b==b.end()){
                if(*cur_a==i) count_a++;
                else break;
            }else if(*cur_a==i && *cur_b==i){
                // c[i]=1;
                continue;
                // a.erase(cur_a,cur_a+1);
                // b.erase(cur_b,cur_b+1);
            }else if(*cur_a==i) count_a++;
            else if(*cur_b==i) count_b++;
            else{
                break;
            }
        }if(count_a<=k/2 && count_b<=k/2 && i==k+1){
            cout<<"YES"<<endl;
        }else{
            cout<<"NO"<<endl;
        }
    }
    return 0;
}

D. Find the Different Ones!

time limit per test5 seconds memory limit per test256 megabytes inputstandard input outputstandard output

You are given an array 𝑎 of 𝑛 integers, and 𝑞 queries.

Each query is represented by two integers 𝑙 and 𝑟 (1≤𝑙≤𝑟≤𝑛). Your task is to find, for each query, two indices 𝑖 and 𝑗 (or determine that they do not exist) such that:

𝑙≤𝑖≤𝑟;𝑙≤𝑗≤𝑟;𝑎𝑖≠𝑎𝑗.

In other words, for each query, you need to find a pair of different elements among 𝑎𝑙,𝑎𝑙+1,…,𝑎𝑟, or report that such a pair does not exist.

Input

The first line of the input contains a single integer 𝑡 (1≤𝑡≤10^4) — the number of test cases. The descriptions of the test cases follow.

The first line of each test case contains a single integer 𝑛 (2≤𝑛≤2⋅10^5) — the length of the array 𝑎.

The second line of each test case contains 𝑛 integers 𝑎1,𝑎2,…,𝑎𝑛 (1≤𝑎𝑖≤10^6) — the elements of the array 𝑎.

The third line of each test case contains a single integer 𝑞 (1≤𝑞≤2⋅10^5) — the number of queries.

The next 𝑞 lines contain two integers each, 𝑙 and 𝑟(1≤𝑙<𝑟≤𝑛) — the boundaries of the query.

It is guaranteed that the sum of the values of 𝑛 across all test cases does not exceed 2⋅10^5. Similarly, it is guaranteed that the sum of the values of 𝑞 across all test cases does not exceed 2⋅10^5.

Output

For each query, output two integers separated by space: 𝑖 and 𝑗(𝑙≤𝑖,𝑗≤𝑟), for which 𝑎𝑖≠𝑎𝑗. If such a pair does not exist, output 𝑖=−1 and 𝑗=−1.

You may separate the outputs for the test cases with empty lines. This is not a mandatory requirement.

Example

input

5
5
1 1 2 1 1
3
1 5
1 2
1 3
6
30 20 20 10 10 20
5
1 2
2 3
2 4
2 6
3 5
4
5 2 3 4
4
1 2
1 4
2 3
2 4
5
1 4 3 2 4
5
1 5
2 4
3 4
3 5
4 5
5
2 3 1 4 2
7
1 2
1 4
1 5
2 4
2 5
3 5
4 5

output

2 3
-1 -1
1 3

2 1
-1 -1
4 2
4 6
5 3

1 2
1 2
2 3
3 2

1 3
2 4
3 4
5 3
5 4

1 2
4 2
1 3
2 3
3 2
5 4
5 4

Code

Time limit exceeded on test 4

#include<iostream>
#include<vector>
#include<map>
#include<algorithm>
using namespace std;
int main(){
    int t,n,q,l,r;
    cin>>t;
    while(t--){
        cin>>n;
        vector<int> v(n+1);
        for(int i=1;i<=n;i++){
            scanf("%d",&v[i]);
        }
        cin>>q;
        while(q--){
            scanf("%d%d",&l,&r);
            unordered_map<int,int> m;
            for(int i=l;i<=r;i++){
                if(!m[v[i]]){
                    m[v[i]]=i;
                }
            }
            vector<pair<int,int>> vp(m.begin(),m.end());
            if(vp.size()>=2){
                cout<<vp[0].second<<" "<<vp[1].second<<endl;
            }else{
                cout<<"-1 -1"<<endl;
            }
        }
    }
    return 0;
}

Codeforces Round 928 (Div. 4)

A. Vlad and the Best of Five

time limit per test: 1 second

memory limit per test: 256 megabytes

input: standard input

output: standard output

Vladislav has a string of length \(5\), whose characters are each either \(\texttt{A}\) or \(\texttt{B}\).

Which letter appears most frequently: \(\texttt{A}\) or \(\texttt{B}\)?

Input

The first line of the input contains an integer \(t\) (\(1 \leq t \leq 32\)) — the number of test cases.

The only line of each test case contains a string of length \(5\) consisting of letters \(\texttt{A}\) and \(\texttt{B}\).

All \(t\) strings in a test are different (distinct).

Output

For each test case, output one letter (\(\texttt{A}\) or \(\texttt{B}\)) denoting the character that appears most frequently in the string.

Example

input

8
ABABB
ABABA
BBBAB
AAAAA
BBBBB
BABAA
AAAAB
BAAAA

output

B
A
B
A
B
A
A
A

Code

#include<bits/stdc++.h>
using namespace std;
int main(){
    int t;
    cin>>t;
    while(t--){
        string s;
        cin>>s;
        int a=0,b=0;
        for(int i=0;i<5;i++){
            if(s[i]=='A')   a++;
            else b++;
        }
        if(a>b) cout<<"A"<<endl;
        else cout<<"B"<<endl;
    }
    return 0;
}

B. Vlad and Shapes

time limit per test: 1 second

memory limit per test: 256 megabytes

input: standard input

output: standard output

Vladislav has a binary square grid of \(n \times n\) cells. A triangle or a square is drawn on the grid with symbols \(\texttt{1}\). As he is too busy being cool, he asks you to tell him which shape is drawn on the grid.

• A triangle is a shape consisting of \(k\) (\(k>1\)) consecutive rows, where the \(i\)-th row has \(2 \cdot i-1\) consecutive characters \(\texttt{1}\), and the central 1s are located in one column. An upside down triangle is also considered a valid triangle (but not rotated by 90 degrees).

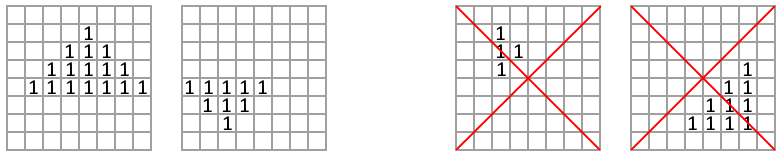Two left pictures contain examples of triangles: \(k=4\), \(k=3\). The two right pictures don't contain triangles.

• A square is a shape consisting of \(k\) (\(k>1\)) consecutive rows, where the \(i\)-th row has \(k\) consecutive characters \(\texttt{1}\), which are positioned at an equal distance from the left edge of the grid.

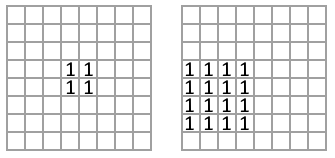Examples of two squares: \(k=2\), \(k=4\).

For the given grid, determine the type of shape that is drawn on it.

Vladislav有一个\(n\times n\)单元格的二进制方格网格。网格上绘制了一个三角形或正方形，符号为\(\texttt{1}\)。由于他太忙于保持酷，他请你告诉他网格上绘制了哪种形状。

• 三角形是由\(k\)(\(k > 1\))个连续行组成的形状，其中第\(i\)行有\(2\cdot i-1\)个连续字符\(\texttt{1}\)，并且中心的1位于一列中。倒三角形也被视为有效的三角形(但不是顺时针旋转90度)。

两幅左图是三角形的示例：\(k=4\)，\(k=3\)。右图的两幅图片不包含三角形。

• 正方形是由\(k\)(\(k > 1\))个连续行组成的形状，其中第\(i\)行有\(k\)个连续字符\(\texttt{1}\)，这些字符与网格的左边缘等距。

两个正方形的示例：\(k=2\)，\(k=4\)。

对于给定的网格，确定绘制在上面的形状类型。

Input

The first line contains a single integer \(t\) (\(1 \leq t \leq 100\)) — the number of test cases.

The first line of each test case contains a single integer \(n\) (\(2 \leq n \leq 10\)) — the size of the grid.

The next \(n\) lines each contain \(n\) characters \(\texttt{0}\) or \(\texttt{1}\).

The grid contains exactly one triangle or exactly one square that contains all the \(\texttt{1}\)s in the grid. It is guaranteed that the size of the triangle or square is greater than \(1\) (i.e., the shape cannot consist of exactly one 1).

输入

第一行包含一个整数 \(t\) (\(1 \leq t \leq 100\)) — 测试用例的数量。

每个测试用例的第一行包含一个整数 \(n\) (\(2 \leq n \leq 10\)) — 网格的大小。

接下来的 \(n\) 行每行包含 \(n\) 个字符 \(\texttt{0}\) 或 \(\texttt{1}\)。

网格中确切地包含一个三角形或一个正方形，其中包含网格中的所有 \(\texttt{1}\)。保证三角形或正方形的大小大于 \(1\)(即，该形状不能仅由一个 1 组成)。

Output

For each test case, output "SQUARE" if all the \(\texttt{1}\)s in the grid form a square, and "TRIANGLE" otherwise (without quotes).

对于每个测试用例，如果网格中的所有1形成一个正方形，则输出“SQUARE”，否则输出“TRIANGLE”(不带引号)。

Example

input

6
3
000
011
011
4
0000
0000
0100
1110
2
11
11
5
00111
00010
00000
00000
00000
10
0000000000
0000000000
0000000000
0000000000
0000000000
1111111110
0111111100
0011111000
0001110000
0000100000
3
111
111
111

output

SQUARE
TRIANGLE
SQUARE
TRIANGLE
TRIANGLE
SQUARE

Code

#include<bits/stdc++.h>
using namespace std;
int main(){
    int t;
    cin>>t;
    while(t--){
        int n;
        cin>>n;
        vector<string> vs(n);
        for(int i=0;i<n;i++){
            cin>>vs[i];
        }
        int line=0;
        while(line<n){
            bool flag=false;
            for(int i=0;i<n;i++){
                if(vs[line][i]=='1'){
                    flag=true;
                    break;
                }
            }
            if(flag)    break;
            line++;
        }
        int cnt1=0,cnt2=0;
        if(line==n){
            cout<<"TRIANGLE"<<endl;
            continue;
        }
        for(int i=0;i<n;i++){
            if(vs[line][i]=='1')    cnt1++;
        }
        for(int i=0;i<n;i++){
            if(vs[line+1][i]=='1')  cnt2++;
        }
        if(cnt1==cnt2)  cout<<"SQUARE"<<endl;
        else cout<<"TRIANGLE"<<endl;
    }
    return 0;
}

C. Vlad and a Sum of Sum of Digits

time limit per test: 0.5 seconds

memory limit per test: 256 megabytes

input: standard input

output: standard output

Please note that the time limit for this problem is only 0.5 seconds per test.

Vladislav wrote the integers from \(1\) to \(n\), inclusive, on the board. Then he replaced each integer with the sum of its digits.

What is the sum of the numbers on the board now?

For example, if \(n=12\) then initially the numbers on the board are:

\[ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12. \] Then after the replacement, the numbers become: \[ 1, 2, 3, 4, 5, 6, 7, 8, 9, 1, 2, 3. \] The sum of these numbers is \(1+2+3+4+5+6+7+8+9+1+2+3=51\). Thus, for \(n=12\) the answer is \(51\).

请注意，此问题的时间限制仅为每个测试0.5秒。

Vladislav在黑板上写下了从\(1\)到\(n\)(包括1和n)的整数。然后，他用其各位数字的总和替换了每个整数。

现在黑板上的数字之和是多少？

例如，如果\(n=12\)，那么最初黑板上的数字是：

\[ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12. \] 然后经过替换后，数字变为： \[ 1, 2, 3, 4, 5, 6, 7, 8, 9, 1, 2, 3. \] 这些数字的和是\(1+2+3+4+5+6+7+8+9+1+2+3=51\)。因此，对于\(n=12\)，答案是\(51\)。

Input

The first line contains an integer \(t\) (\(1 \leq t \leq 10^4\)) — the number of test cases.

The only line of each test case contains a single integer \(n\) (\(1 \leq n \leq 2 \cdot 10^5\)) — the largest number Vladislav writes.

输入

第一行包含一个整数 \(t\)(\(1 \leq t \leq 10^4\))表示测试用例的数量。

每个测试用例的唯一一行包含一个整数 \(n\)(\(1 \leq n \leq 2 \cdot 10^5\))表示Vladislav写下的最大数字。

Output

For each test case, output a single integer — the sum of the numbers at the end of the process.

对于每个测试用例，输出一个整数 - 过程结束时数字的总和。

Example

input

7
12
1
2
3
1434
2024
200000

output

51
1
3
6
18465
28170
4600002

Code1

RunTime Error

#include<bits/stdc++.h>
using namespace std;

// int get(int num){
//     int res=0;
//     while(num){
//         res+=num%10;
//         res/=10;
//     }
//     return res;
// }

int main(){
    int t;
    cin>>t;
    vector<int> v(10);
    for(int i=0;i<10;i++){
        v[i]=i;
    }
    for(int j=1;j<5;j++){
        int d=pow(10,j);
        for(int i=1;i<10;i++){
            for(int k=0;k<d;k++){
                v.emplace_back(v[k]+i);
            }
        }
    }
    for(int i=1;i<3;i++){
        for(int k=0;k<10000;k++){
            v.emplace_back(v[k]+i);
        }
    }
    int sum=0;
    for(int i=0;i<10000;i++){
        sum+=v[i];
        v[i]=sum;
    }
    while(t--){
        int n;
        cin>>n;
        cout<<v[n]<<endl;
        // int sum=0;
        // for(int i=1;i<=n;i++){
        //     sum+=get(i);
        // }
        // cout<<sum;
        // for(int i=0;i<1000;i++){
        //     cout<<" "<<i<<'='<<v[i];
        // }
    }
    return 0;
}

Code

#include<bits/stdc++.h>
using namespace std;
int main(){
    int t;
    cin>>t;
    vector<int> v(10);
    for(int i=0;i<10;i++){
        v[i]=i;
    }
    for(int j=1;j<5;j++){
        int d=pow(10,j);
        for(int i=1;i<10;i++){
            for(int k=0;k<d;k++){
                v.emplace_back(v[k]+i);
            }
        }
    }
    for(int i=1;i<2;i++){
        for(int k=0;k<100000;k++){
            v.emplace_back(v[k]+i);
        }
    }
    // cout<<v.size()<<endl;
    v.emplace_back(2);
    // for(int i=190244;i<190332;i++){
    //     cout<<i<<"="<<v[i]<<" ";
    // }
    for(int i=1;i<=200000;i++){
        v[i]+=v[i-1];
    }
    // cout<<"&"<<endl;
    // for(int i=190244;i<190332;i++){
    //     cout<<i<<"="<<v[i]<<" ";
    // }
    while(t--){
        int n;
        cin>>n;
        cout<<v[n]<<endl;
    }
    return 0;
}

D. Vlad and Division

time limit per test: 2 seconds

memory limit per test: 256 megabytes

input: standard input

output: standard output

Vladislav has \(n\) non-negative integers, and he wants to divide all of them into several groups so that in any group, any pair of numbers does not have matching bit values among bits from \(1\)-st to \(31\)-st bit (i.e., considering the \(31\) least significant bits of the binary representation).

For an integer \(k\), let \(k_2(i)\) denote the \(i\)-th bit in its binary representation (from right to left, indexing from 1). For example, if \(k=43\), since \(43=101011_2\), then \(43_2(1)=1\), \(43_2(2)=1\), \(43_2(3)=0\), \(43_2(4)=1\), \(43_2(5)=0\), \(43_2(6)=1\), \(43_2(7)=0\), \(43_2(8)=0, \dots, 43_2(31)=0\).

Formally, for any two numbers \(x\) and \(y\) in the same group, the condition \(x_2(i) \neq y_2(i)\) must hold for all \(1 \leq i < 32\).

What is the minimum number of groups Vlad needs to achieve his goal? Each number must fall into exactly one group.

Vladislav有\(n\)个非负整数，他想将它们全部分成若干组，以便在任何一组中，任意一对数字在从第\(1\)位到第\(31\)位的比特中没有匹配的比特值(即考虑二进制表示的\(31\)个最低有效位)。

对于一个整数\(k\)，设\(k_2(i)\)表示其二进制表示中的第\(i\)位(从右向左，从1开始索引)。例如，如果\(k=43\)，因为\(43=101011_2\)，那么\(43_2(1)=1\)，\(43_2(2)=1\)，\(43_2(3)=0\)，\(43_2(4)=1\)，\(43_2(5)=0\)，\(43_2(6)=1\)，\(43_2(7)=0\)，\(43_2(8)=0, \dots, 43_2(31)=0\)。

形式上，对于同一组中的任意两个数字\(x\)和\(y\)，必须满足条件\(x_2(i) \neq y_2(i)\)，对于所有的\(1 \leq i < 32\)。

Vlad需要达到他的目标所需的最小组数是多少？每个数字必须恰好属于一组。

Input

The first line contains a single integer \(t\) (\(1 \leq t \leq 10^4\)) — the number of test cases.

The first line of each test case contains a single integer \(n\) (\(1 \leq n \leq 2 \cdot 10^5\)) — the total number of integers.

The second line of each test case contains \(n\) given integers \(a_1, \ldots, a_n\) (\(0 \leq a_j < 2^{31}\)).

The sum of \(n\) over all test cases in a test does not exceed \(2 \cdot 10^5\).

输入

第一行包含一个整数 \(t\) (\(1 \leq t \leq 10^4\)) — 测试用例的数量。

每个测试用例的第一行包含一个整数 \(n\) (\(1 \leq n \leq 2 \cdot 10^5\)) — 整数的总数。

每个测试用例的第二行包含 \(n\) 个给定的整数 \(a_1, \ldots, a_n\) (\(0 \leq a_j < 2^{31}\))。

一个测试中所有测试用例中 \(n\) 的总和不超过 \(2 \cdot 10^5\)。

Output

For each test case, output a single integer  — the minimum number of groups required to satisfy the condition.

输出

对于每个测试案例，输出一个整数，即满足条件所需的最小组数。

Example

input

9
4
1 4 3 4
2
0 2147483647
5
476319172 261956880 2136179468 1671164475 1885526767
3
1335890506 811593141 1128223362
4
688873446 627404104 1520079543 1458610201
4
61545621 2085938026 1269342732 1430258575
4
0 0 2147483647 2147483647
3
0 0 2147483647
8
1858058912 289424735 1858058912 2024818580 1858058912 289424735 122665067 289424735

output

4
1
3
2
2
3
2
2
4

Note

In the first test case, any two numbers have the same last \(31\) bits, so we need to place each number in its own group.

In the second test case, \(a_1=0000000000000000000000000000000_2\), \(a_2=1111111111111111111111111111111_2\) so they can be placed in the same group because \(a_1(i) \ne a_2(i)\) for each \(i\) between \(1\) and \(31\), inclusive.

注意

在第一个测试用例中，任意两个数字的最后31位相同，因此我们需要将每个数字放在自己的组中。

在第二个测试用例中，\(a_1=0000000000000000000000000000000_2\)，\(a_2=1111111111111111111111111111111_2\)，因此它们可以放在同一组中，因为对于每个\(i\)(\(1\)到\(31\)，包括\(1\)和\(31\))，\(a_1(i) \ne a_2(i)\)。

Code

#include<bits/stdc++.h>
using namespace std;
int main(){
    int t;
    cin>>t;
    while(t--){
        int n;
        cin>>n;
        int count=n;
        map<int,int> m;
        while(n--){
            int temp;
            cin>>temp;
            if(!m[2147483647-temp]){ //不存在
                m[temp]++;
            }else if(m[2147483647-temp]>0){
                m[2147483647-temp]--;
                count--;
            }
            // for(auto &k:m){
            //     cout<<k.first<<","<<k.second<<endl;
            // }
        }
        cout<<count<<endl;
    }
    return 0;
}

E. Vlad and an Odd Ordering

time limit per test: 2 seconds

memory limit per test: 256 megabytes

input: standard input

output: standard output

Vladislav has \(n\) cards numbered \(1, 2, \dots, n\). He wants to lay them down in a row as follows:

• First, he lays down all the odd-numbered cards from smallest to largest.
• Next, he lays down all cards that are twice an odd number from smallest to largest (i.e. \(2\) multiplied by an odd number).
• Next, he lays down all cards that are \(3\) times an odd number from smallest to largest (i.e. \(3\) multiplied by an odd number).
• Next, he lays down all cards that are \(4\) times an odd number from smallest to largest (i.e. \(4\) multiplied by an odd number).
• And so on, until all cards are laid down.

What is the \(k\)-th card he lays down in this process? Once Vladislav puts a card down, he cannot use that card again.

Vladislav有\(n\)张编号为\(1, 2, \dots, n\)的卡片。他想按照以下顺序将它们排成一排：

• 首先，他按从小到大的顺序放下所有奇数编号的卡片。
• 接下来，他按从小到大的顺序放下所有是奇数的两倍的卡片(即奇数乘以\(2\))。
• 接下来，他按从小到大的顺序放下所有是奇数的三倍的卡片(即奇数乘以\(3\))。
• 接下来，他按从小到大的顺序放下所有是奇数的四倍的卡片(即奇数乘以\(4\))。
• 依此类推，直到所有卡片都被放下。

在这个过程中，他放下的第\(k\)张卡片是哪一张？一旦Vladislav放下一张卡片，他就不能再使用那张卡片。

Input

The first line contains an integer \(t\) (\(1 \leq t \leq 5 \cdot 10^4\)) — the number of test cases.

The only line of each test case contains two integers \(n\) and \(k\) (\(1 \leq k \leq n \leq 10^9\)) — the number of cards Vlad has, and the position of the card you need to output.

输入

第一行包含一个整数 \(t\) (\(1 \leq t \leq 5 \cdot 10^4\)) — 测试用例的数量。

每个测试用例的唯一一行包含两个整数 \(n\) 和 \(k\) (\(1 \leq k \leq n \leq 10^9\)) — 弗拉德拥有的卡片数量，以及需要输出的卡片位置。

Output

For each test case, output a single integer — the \(k\)-th card Vladislav lays down.

对于每个测试用例，输出一个整数 - 弗拉迪斯拉夫放下的第\(k\)张卡片。

Example

input

11
7 1
7 2
7 3
7 4
7 5
7 6
7 7
1 1
34 14
84 19
1000000000 1000000000

output

1
3
5
7
2
6
4
1
27
37
536870912

Note

In the first seven test cases, \(n=7\). Vladislav lays down the cards as follows:

• First — all the odd-numbered cards in the order \(1\), \(3\), \(5\), \(7\).
• Next — all cards that are twice an odd number in the order \(2\), \(6\).
• Next, there are no remaining cards that are \(3\) times an odd number. (Vladislav has only one of each card.)
• Next — all cards that are \(4\) times an odd number, and there is only one such card: \(4\).
• There are no more cards left, so Vladislav stops.

Thus the order of cards is \(1\), \(3\), \(5\), \(7\), \(2\), \(6\), \(4\).

注意

在前七个测试案例中，\(n=7\)。弗拉迪斯拉夫按照以下顺序放置卡片：

• 第一张 - 所有奇数编号的卡片，按顺序为 \(1\)、\(3\)、\(5\)、\(7\)。
• 接下来 - 所有是奇数的两倍的卡片，按顺序为 \(2\)、\(6\)。
• 接下来，没有剩余的卡片是奇数的三倍。(弗拉迪斯拉夫每张卡片只有一张。)
• 接下来 - 所有是奇数的四倍的卡片，只有一张这样的卡片：\(4\)。
• 没有更多卡片了，所以弗拉迪斯拉夫停止。

因此，卡片的顺序是 \(1\)、\(3\)、\(5\)、\(7\)、\(2\)、\(6\)、\(4\)。

Code0

本来想用这个方法做的。但是时间效率极低。

#include<bits/stdc++.h>
using namespace std;

int t,n,k;

void func(){
    vector<int> v(n+1,1);
    for(int times=1;times<=n;times+=1){
        for(int i=times;i<=n;i+=times*2){
            if(v[i]){
                v[i]=0;
                k--;
            }
            if(k==0){
                cout<<i<<endl;
                return;
            }
        }
    }
}

int main(){
    cin>>t;
    while(t--){
        cin>>n>>k;
        func();
    }
    return 0;
}

Code1

WA

#include<bits/stdc++.h>
using namespace std;
int main(){
    int t;
    cin>>t;
    while(t--){
        int n,k,times=0;
        cin>>n>>k;
        while(true){
            if(k>n/2){
                k-=n/2;
                n-=n/2;
                times++;
            }else break;
            if(k==1)    break;
        }
        k=k*2-1;
        k*=pow(2,times);
        if(k!=1) cout<<k<<endl;
        else cout<<k/2<<endl;
    }
    return 0;
}

Code2

#include<bits/stdc++.h>
using namespace std;
int main(){
    int t;
    cin>>t;
    while(t--){
        int n,k,times=0;
        cin>>n>>k;
        while(true){
            if(k>(n+1)/2){
                k-=(n+1)/2;
                n-=(n+1)/2;
                times++;
            }else break;
            // cout<<"n="<<n<<",k="<<k<<endl;
            if(k==1 && n==1)    break;
        }
        k=k*2-1;
        k*=pow(2,times);
        // if(k==1 && n==1) k/=2;
        cout<<k<<endl;
    }
    return 0;
}

G. Vlad and Trouble at MIT

time limit per test: 1 second

memory limit per test: 256 megabytes

input: standard input

output: standard output

Vladislav has a son who really wanted to go to MIT. The college dormitory at MIT (Moldova Institute of Technology) can be represented as a tree with \(n\) vertices, each vertex being a room with exactly one student. A tree is a connected undirected graph with \(n\) vertices and \(n-1\) edges.

Tonight, there are three types of students:

• students who want to party and play music (marked with \(\texttt{P}\)),
• students who wish to sleep and enjoy silence (marked with \(\texttt{S}\)), and
• students who don't care (marked with \(\texttt{C}\)).

Initially, all the edges are thin walls which allow music to pass through, so when a partying student puts music on, it will be heard in every room. However, we can place some thick walls on any edges — thick walls don't allow music to pass through them.

The university wants to install some thick walls so that every partying student can play music, and no sleepy student can hear it.

Because the university lost a lot of money in a naming rights lawsuit, they ask you to find the minimum number of thick walls they will need to use.

Vladislav有一个儿子，他非常想去MIT。 MIT(摩尔多瓦工学院)的学生宿舍可以被表示为一个树，有\(n\)个顶点，每个顶点是一个只有一个学生的房间。树是一个有\(n\)个顶点和\(n-1\)条边的连通无向图。

今晚，有三种类型的学生：

• 想要聚会和播放音乐的学生(标记为\(\texttt{P}\))，
• 希望睡觉和享受安静的学生(标记为\(\texttt{S}\))，
• 不在乎的学生(标记为\(\texttt{C}\))。

最初，所有的边都是薄墙，允许音乐传播，因此当一个聚会的学生放音乐时，每个房间都会听到。然而，我们可以在任意边上放置一些厚墙——厚墙不允许音乐通过。

学校想要安装一些厚墙，以便每个聚会的学生都可以播放音乐，而没有任何想要睡觉的学生能听到。

因为学校在一个商标诉讼中损失了很多钱，他们要求你找出他们需要使用的最少数量的厚墙。

Input

The first line contains a single integer \(t\) (\(1 \leq t \leq 1000\)) — the number of test cases.

The first line of each test case contains an integer \(n\) (\(2 \leq n \leq 10^5\)) — the number of vertices in the tree.

The second line of each test case contains \(n-1\) integers \(a_2, \dots , a_n\) (\(1 \leq a_i &lt; i\)) — it means there is an edge between \(i\) and \(a_i\) in the tree.

The third line of each test case contains a string \(s\) of length \(n\) consisting of characters \(\texttt{P}\), \(\texttt{S}\), and \(\texttt{C}\), denoting that student \(i\) is of type \(s_i\).

The sum of \(n\) over all test cases does not exceed \(10^5\).

输入

第一行包含一个整数 \(t\) (\(1 \leq t \leq 1000\)) — 测试用例的数量。

每个测试用例的第一行包含一个整数 \(n\) (\(2 \leq n \leq 10^5\)) — 树中顶点的数量。

每个测试用例的第二行包含 \(n-1\) 个整数 \(a_2, \dots , a_n\) (\(1 \leq a_i &lt; i\)) — 表示树中 \(i\) 和 \(a_i\) 之间有一条边。

每个测试用例的第三行包含一个长度为 \(n\) 的字符串 \(s\)，由字符 \(\texttt{P}\)、\(\texttt{S}\) 和 \(\texttt{C}\) 组成，表示学生 \(i\) 的类型为 \(s_i\)。

所有测试用例中 \(n\) 的总和不超过 \(10^5\)。

Output

For each test case, output a single integer — the minimum number of thick walls needed.

输出

对于每个测试用例，输出一个整数 - 所需的最小厚墙数量。

Example

input

3
3
1 1
CSP
4
1 2 2
PCSS
4
1 2 2
PPSS

output

1
1
2

Note

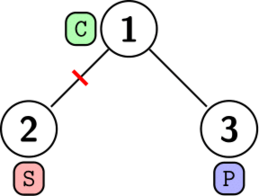
In the first case, we can install one thick wall between rooms \(1\) and \(2\), as shown below. We cannot install \(0\) walls, since then the music from room 3 will reach room 2 where a student wants to sleep, so the answer is \(1\). There are other valid solutions.

注意

在第一种情况下，我们可以在房间\(1\)和\(2\)之间安装一堵厚墙，如下所示。我们不能安装\(0\)面墙，因为这样房间\(3\)的音乐会传到一个想要睡觉的学生的房间\(2\)，所以答案是\(1\)。还有其他有效的解决方案。

Code

失败

#include<bits/stdc++.h>
using namespace std;

struct type{ int p,s,c; };
int cnt;
vector<vector<int>> vv;
vector<type> dp;
string str;

// char dfs(int now){
//     if(vv[now].size()==0)   return str[now];
//     if(str[now]=='C'){
//         str[now]=dfs(vv[now][0]);
//         for(int i=1;i<vv[now].size();i++){
//             if(dfs(vv[now][i])=='P'&&str[now]=='S') cnt++;
//             if(dfs(vv[now][i])=='S'&&str[now]=='P') cnt++;
//             // cout<<",now="<<now<<",k="<<vv[now][i]<<",cnt="<<cnt<<endl;
//         }
//     } else if(str[now]=='P'){
//         for(auto& k:vv[now]){
//             if(dfs(k)=='S') cnt++;
//             // cout<<",now="<<now<<",k="<<k<<",cnt="<<cnt<<endl;
//         }
//     } else{
//         for(auto& k:vv[now]){
//             if(dfs(k)=='P') cnt++;
//             // cout<<",now="<<now<<",k="<<k<<",cnt="<<cnt<<endl;
//         }
//     }
//     return str[now];
// }

void dfs(int now){
    
}

void solve(){
    int n;
    cin>>n;
    cnt=0;
    vv.clear();
    vv.resize(n+1);
    for(int i=2;i<=n;i++){
        int temp;
        cin>>temp;
        vv[temp].emplace_back(i);
    }

    // for(int i=0;i<vv.size();i++){
    //     cout<<i;
    //     for(int j=0;j<vv[i].size();j++){
    //         cout<<" "<<vv[i][j];
    //     }
    //     cout<<endl;
    // }

    cin>>str;
    str="0"+str;
    dfs(1);
    cout<<cnt<<endl;
}

int main(){
    int t;
    cin>>t;
    while(t--){
        solve();
    }
    return 0;
}

Educational Codeforces Round 163 (Rated for Div. 2)

A. Special Characters

time limit per test: 2 seconds

memory limit per test: 256 megabytes

input: standard input

output: standard output

You are given an integer \(n\).

Your task is to build a string of uppercase Latin letters. There must be exactly \(n\) special characters in this string. Let's call a character special if it is equal to exactly one of its neighbors.

For example, there are \(6\) special characters in the AAABAACC string (at positions: \(1\), \(3\), \(5\), \(6\), \(7\) and \(8\)).

Print any suitable string or report that there is no such string.

Input

The first line contains a single integer \(t\) (\(1 \le t \le 50\)) — the number of test cases.

The only line of each test case contains a single integer \(n\) (\(1 \le n \le 50\)).

Output

For each test case, print the answer as follows:

• if there is no suitable string, print one line containing the string NO;
• otherwise, print two lines. The first line should contain the string YES; on the second line print a string of length at most \(200\) — the answer itself (it can be shown that if some answers exist, then there is an answer of length at most \(200\)). If there are several solutions, print any of them.

Example

input

3
6
1
2

output

YES
AAABAACC
NO
YES
MM

Code

#include<bits/stdc++.h>
using namespace std;

void solve(){
    int n;
    cin>>n;
    if(n%2==1){
        cout<<"NO\n";
    }else{
        cout<<"YES\n";
        bool flag=true;
        for(int i=0;i<n/2;i++){
            if(flag){
                cout<<"AA";
                flag=false;
            }else{
                cout<<"BB";
                flag=true;
            }
        }
        cout<<"\n";
    }

}


int main(){
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);
    int t;
    cin>>t;
    while(t--){
        solve();
    }
    return 0;
}

B. Array Fix

time limit per test: 2 seconds

memory limit per test: 256 megabytes

input: standard input

output: standard output

You are given an integer array \(a\) of length \(n\).

You can perform the following operation any number of times (possibly zero): take any element of the array \(a\), which is at least \(10\), delete it, and instead insert the digits that element consisted of in the same position, in order they appear in that element.

For example:

• if we apply this operation to the \(3\)-rd element of the array \([12, 3, 45, 67]\), then the array becomes \([12, 3, 4, 5, 67]\).
• if we apply this operation to the \(2\)-nd element of the array \([2, 10]\), then the array becomes \([2, 1, 0]\).

Your task is to determine whether it is possible to make \(a\) sorted in non-descending order using the aforementioned operation any number of times (possibly zero). In other words, you have to determine if it is possible to transform the array \(a\) in such a way that \(a_1 \le a_2 \le \dots \le a_k\), where \(k\) is the current length of the array \(a\).

Input

The first line contains a single integer \(t\) (\(1 \le t \le 10^3\)) — the number of test cases.

Each test case consists of two lines:

• the first line contains a single integer \(n\) (\(2 \le n \le 50\)).
• the second line contains \(n\) integers \(a_1, a_2, \dots, a_n\) (\(0 \le a_i \le 99\)).

Output

For each test case, print YES if it is possible to make \(a\) sorted in non-decreasing order using the aforementioned operation; otherwise, print NO.

You can print each letter in any case. For example, yes, Yes, YeS will all be recognized as a positive answer.

Example

input

3
4
12 3 45 67
3
12 28 5
2
0 0

output

YES
NO
YES

Note

In the first example, you can split the first element, then the array becomes \([1, 2, 3, 45, 67]\).

In the second example, there is no way to get a sorted array.

In the third example, the array is already sorted.

Code1-WA

#include<bits/stdc++.h>
using namespace std;

int nums[100];
int dp[100][2];

void solve(){
    int n;
    cin>>n;
    memset(dp,0,sizeof(dp));
    for(int i=0;i<n;i++){
        cin>>nums[i];
    }
    for(int i=0;i<n;i++){
        if(i==0){
            dp[i][0]=true;
            if(nums[i]%10<nums[i]/10) dp[i][1]=false;
            else dp[i][1]=true;
        }else{
            if(nums[i]/10){
                if(nums[i-1]/10){ // 43 23
                    dp[i][0]=nums[i]>=nums[i-1] && dp[i-1][0];
                    dp[i][1]=nums[i]/10>=nums[i-1]%10 && dp[i-1][1];
                }else{ // 2 43
                    dp[i][0]=nums[i]>=nums[i-1] && dp[i-1][0];
                    dp[i][1]=nums[i]/10>=nums[i-1] && dp[i-1][1];
                }
                if(nums[i]/10>nums[i]%10) dp[i][1]=false;
            }else{
                if(nums[i-1]/10){ // 23 1
                    dp[i][0]=nums[i]>=nums[i-1]%10 && dp[i-1][1];
                    dp[i][1]=nums[i]>=nums[i-1]%10 && dp[i-1][1];
                }else{ // 2 3
                    dp[i][0]=nums[i]>=nums[i-1] && dp[i-1][0];
                    dp[i][1]=nums[i]>=nums[i-1] && dp[i-1][0];
                }
            }
            // if(nums[i]>nums[i-1]){
            //     dp[i][0]=max(dp[i][0],dp[i-1][0]);
            // }
            // if(nums[i]>nums[i-1]%10){
            //     dp[i][0]=max(dp[i][0],dp[i-1][1]);
            // }
            // if(nums[i]%10<nums[i]/10){
            //     if(nums[i]/10>nums[i-1]%10){
            //         dp[i][1]=max(dp[i][1],dp[i-1][1]);
            //     }else{
            //         dp[i][1]=false;
            //     }
            // }else{
            //     dp[i][1]=false;
            // }
        }
    }
    // for(int i=0;i<n;i++){
    //     cout<<dp[i][0]<<",";
    // }cout<<endl;
    // for(int i=0;i<n;i++){
    //     cout<<dp[i][1]<<",";
    // }cout<<endl;
    if(dp[n-1][0] || dp[n-1][1]){
        cout<<"YES\n";
    }else{
        cout<<"NO\n";
    }
}


int main(){
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);
    int t;
    cin>>t;
    while(t--)
        solve();
    return 0;
}

Code2-AC

#include<bits/stdc++.h>
using namespace std;

int nums[100];
int dp[100][2];

bool check(int n){
    int temp;
    for(int i=0;i<n;i++){
        if(i==0){
            if(nums[0]/10>nums[0]%10) temp=nums[0];
            else temp=nums[0]%10;
        }else{
            if(nums[i]/10<=nums[i]%10 && nums[i]/10>=temp) temp=nums[i]%10;
            else if(nums[i]>=temp) temp=nums[i];
            else return false;
        }
    }
    return true;
}

void solve(){
    int n;
    cin>>n;
    memset(dp,0,sizeof(dp));
    for(int i=0;i<n;i++){
        cin>>nums[i];
    }
    if(check(n)) cout<<"YES\n";
    else cout<<"NO\n";
    // for(int i=0;i<n;i++){
    //     if(i==0){
    //         dp[i][0]=true;
    //         if(nums[i]%10<nums[i]/10) dp[i][1]=false;
    //         else dp[i][1]=true;
    //     }else{
    //         if(!dp[i-1][0] && !dp[i-1][1]) break;
    //         if(dp[i-1][0] && !dp[i-1][1]){
    //         }
    //         if(nums[i]/10){
    //             if(nums[i-1]/10){ // 43 23
    //                 dp[i][0]=nums[i]>=nums[i-1] && dp[i-1][0];
    //                 dp[i][1]=nums[i]/10>=nums[i-1]%10 && dp[i-1][1];
    //             }else{ // 2 43
    //                 dp[i][0]=nums[i]>=nums[i-1] && dp[i-1][0];
    //                 dp[i][1]=nums[i]/10>=nums[i-1] && dp[i-1][1];
    //             }
    //             if(nums[i]/10>nums[i]%10) dp[i][1]=false;
    //         }else{
    //             if(nums[i-1]/10){ // 23 1
    //                 dp[i][0]=nums[i]>=nums[i-1]%10 && dp[i-1][1];
    //                 dp[i][1]=nums[i]>=nums[i-1]%10 && dp[i-1][1];
    //             }else{ // 2 3
    //                 dp[i][0]=nums[i]>=nums[i-1] && dp[i-1][0];
    //                 dp[i][1]=nums[i]>=nums[i-1] && dp[i-1][0];
    //             }
    //         }
    //     }
    // }
    // for(int i=0;i<n;i++){
    //     cout<<dp[i][0]<<",";
    // }cout<<endl;
    // for(int i=0;i<n;i++){
    //     cout<<dp[i][1]<<",";
    // }cout<<endl;
    // if(dp[n-1][0] || dp[n-1][1]){
    //     cout<<"YES\n";
    // }else{
    //     cout<<"NO\n";
    // }
}


int main(){
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);
    int t;
    cin>>t;
    while(t--)
        solve();
    return 0;
}

C. Arrow Path

time limit per test: 2 seconds

memory limit per test: 256 megabytes

input: standard input

output: standard output

There is a grid, consisting of \(2\) rows and \(n\) columns. The rows are numbered from \(1\) to \(2\) from top to bottom. The columns are numbered from \(1\) to \(n\) from left to right. Each cell of the grid contains an arrow pointing either to the left or to the right. No arrow points outside the grid.

There is a robot that starts in a cell \((1, 1)\). Every second, the following two actions happen one after another:

1. Firstly, the robot moves left, right, down or up (it can't try to go outside the grid, and can't skip a move);
2. then it moves along the arrow that is placed in the current cell (the cell it ends up after its move).

Your task is to determine whether the robot can reach the cell \((2, n)\).

Input

The first line contains a single integer \(t\) (\(1 \le t \le 10^4\)) — the number of test cases.

The first line of each test case contains a single integer (\(2 \le n \le 2 \cdot 10^5\)).

The second line contains a string consisting of exactly \(n\) characters < and/or > — the first row of the grid.

The third line contains a string consisting of exactly \(n\) characters < and/or > — the second row of the grid.

Additional constraints on the input:

• \(n\) is even;
• there are no arrows pointing outside the grid;
• the sum of \(n\) over all test cases doesn't exceed \(2 \cdot 10^5\).

Output

For each test case, print YES if the robot can reach the cell \((2, n)\); otherwise, print NO.

You can print each letter in any case. For example, yes, Yes, YeS will all be recognized as positive answer.

Example

input

4
4
>><<
>>><
2
><
><
4
>>><
>><<
6
>><<><
><>>><

output

YES
YES
NO
YES

Code1-WA

#include<bits/stdc++.h>
using namespace std;



string mp[2];
int vis[2][100000];
int dx[4]={0,0,1,-2};
int dy[4]={1,-2,1,0};

bool solve(){
    int n;
    cin>>n;
    cin>>mp[0]>>mp[1];
    // mp[0]=' '+mp[0];
    // mp[1]=' '+mp[1];
    queue<pair<int,int>> q;
    memset(vis,0,sizeof(vis));
    q.push({0,0});
    vis[0][0]=true;
    while(!q.empty()){
        int x=q.front().first,y=q.front().second;
        // cout<<endl;
        // cout<<x<<","<<y<<endl;
        q.pop();
        for(int i=0;i<4;i++){
            x+=dx[i];
            y+=dy[i];
            if(x<=1 && x>=0 && y>=0 && y<n && !vis[x][y+((mp[x][y]=='<')?-1:1)]){
                // cout<<((mp[x][y]=='<')?-1:1)<<endl;
                // cout<<x<<","<<y+((mp[x][y]=='<')?-1:1)<<endl;
                if(x==1 && y+((mp[x][y]=='<')?-1:1)==n-1) {
                // cout<<y+((vis[x][y]=='<')?-1:1)<<endl;
                return true;}
                q.push({x,y+((mp[x][y]=='<')?-1:1)});
                vis[x][y+((mp[x][y]=='<')?-1:1)]=true;
            }
        }
    }
    return false;
}

int main(){
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);
    int t;
    cin>>t;
    while(t--)
        if(solve()) cout<<"YES\n";
        else cout<<"NO\n";
    return 0;
}

Code2-AC

#include<bits/stdc++.h>
using namespace std;



string mp[2];
int vis[2][200010];
int dx[4]={0,0,1,-2};
int dy[4]={1,-2,1,0};

bool solve(){
    int n;
    cin>>n;
    cin>>mp[0]>>mp[1];
    // mp[0]=' '+mp[0];
    // mp[1]=' '+mp[1];
    queue<pair<int,int>> q;
    memset(vis,0,sizeof(vis));
    q.push({0,0});
    vis[0][0]=true;
    while(!q.empty()){
        int x=q.front().first,y=q.front().second;
        // cout<<endl;
        // cout<<x<<","<<y<<endl;
        q.pop();
        for(int i=0;i<4;i++){
            x+=dx[i];
            y+=dy[i];
            if(x<=1 && x>=0 && y>=0 && y<n && !vis[x][y+((mp[x][y]=='<')?-1:1)]){
                // cout<<((mp[x][y]=='<')?-1:1)<<endl;
                // cout<<x<<","<<y+((mp[x][y]=='<')?-1:1)<<endl;
                if(x==1 && y+((mp[x][y]=='<')?-1:1)==n-1) {
                // cout<<y+((vis[x][y]=='<')?-1:1)<<endl;
                return true;}
                q.push({x,y+((mp[x][y]=='<')?-1:1)});
                vis[x][y+((mp[x][y]=='<')?-1:1)]=true;
            }
        }
    }
    return false;
}

int main(){
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);
    int t;
    cin>>t;
    while(t--)
        if(solve()) cout<<"YES\n";
        else cout<<"NO\n";
    return 0;
}

Codeforces Round 934 (Div. 2)

A. Destroying Bridges

time limit per test: 1 second

memory limit per test: 256 megabytes

input: standard input

output: standard output

There are \(n\) islands, numbered \(1, 2, \ldots, n\). Initially, every pair of islands is connected by a bridge. Hence, there are a total of \(\frac{n (n - 1)}{2}\) bridges.

Everule lives on island \(1\) and enjoys visiting the other islands using bridges. Dominater has the power to destroy at most \(k\) bridges to minimize the number of islands that Everule can reach using (possibly multiple) bridges.

Find the minimum number of islands (including island \(1\)) that Everule can visit if Dominater destroys bridges optimally.

Input

Each test contains multiple test cases. The first line contains a single integer \(t\) (\(1 \leq t \leq 10^3\)) — the number of test cases. The description of the test cases follows.

The first and only line of each test case contains two integers \(n\) and \(k\) (\(1 \le n \le 100\), \(0 \le k \le \frac{n \cdot (n - 1)}{2}\)).

Output

For each test case, output the minimum number of islands that Everule can visit if Dominater destroys bridges optimally.

Example

**input

6
2 0
2 1
4 1
5 10
5 3
4 4

output

2
1
4
1
5
1

Code-PreAC

240316

#include<bits/stdc++.h>
using namespace std;

void solve(){
    int n,k;
    cin>>n>>k;
    if(k>=n-1){
        cout<<"1\n";
        return;
    }
    int l=0;
    int r=n;
    while(l<r){
        // cout<<l<<","<<r<<endl;
        int mid=(l+r+1)/2;
        if(mid*(n-mid)>k) r=mid-1;
        else l=mid;
    }
    cout<<n-r<<"\n";
}



int main(){
    int t;
    cin>>t;
    while(t--)
        solve();
    return 0;
}

B. Equal XOR

time limit per test: 1 second

memory limit per test: 256 megabytes

input: standard input

output: standard output

You are given an array \(a\) of length \(2n\), consisting of each integer from \(1\) to \(n\) exactly twice.

You are also given an integer \(k\) ($1 k $ ).

You need to find two arrays \(l\) and \(r\) each of length \(\mathbf{2k}\) such that:

• \(l\) is a subset\(^\dagger\) of \([a_1, a_2, \ldots a_n]\)
• \(r\) is a subset of \([a_{n+1}, a_{n+2}, \ldots a_{2n}]\)
• bitwise XOR of elements of \(l\) is equal to the bitwise XOR of elements of \(r\); in other words, \(l_1 \oplus l_2 \oplus \ldots \oplus l_{2k} = r_1 \oplus r_2 \oplus \ldots \oplus r_{2k}\)

It can be proved that at least one pair of \(l\) and \(r\) always exists. If there are multiple solutions, you may output any one of them.

\(^\dagger\) A sequence \(x\) is a subset of a sequence \(y\) if \(x\) can be obtained by deleting several (possibly none or all) elements of \(y\) and rearranging the elements in any order. For example, \([3,1,2,1]\), \([1, 2, 3]\), \([1, 1]\) and \([3, 2]\) are subsets of \([1, 1, 2, 3]\) but \([4]\) and \([2, 2]\) are not subsets of \([1, 1, 2, 3]\).

给定长度为\(2n\)的数组\(a\)，由\(1\)到\(n\)的每个整数恰好两次组成。

还给定一个整数\(k\)(\(1 \leq k \leq \lfloor \frac{n} {2} \rfloor\))。

需要找到两个长度为\(\mathbf{2k}\)的数组\(l\)和\(r\)，满足以下条件：

• \(l\)是\([a &#95; 1, a &#95; 2, \ldots a &#95; n]\)的子集\(^\dagger\)
• \(r\)是\([a &#95; {n+1}, a &#95; {n+2}, \ldots a &#95; {2n}]\)的子集
• \(l\)元素的按位异或等于\(r\)元素的按位异或；换句话说，\(l &#95; 1 \oplus l &#95; 2 \oplus \ldots l &#95; {2k} = r &#95; 1 \oplus r &#95; 2 \oplus \ldots r &#95; {2k}\)

可以证明至少一对\(l\)和\(r\)总是存在。如果有多个解，可以输出任意一个。

\(^\dagger\) 如果序列\(x\)可以通过删除序列\(y\)的若干(可能为零或全部)元素并以任意顺序重新排列元素得到，则序列\(x\)是序列\(y\)的子集。例如，\([3,1,2,1]\)，\([1, 2, 3]\)，\([1, 1]\)和\([3, 2]\)是\([1, 1, 2, 3]\)的子集，但\([4]\)和\([2, 2]\)不是\([1, 1, 2, 3]\)的子集。

Input

Each test contains multiple test cases. The first line contains a single integer \(t\) (\(1 \leq t \leq 5000\)) — the number of test cases. The description of the test cases follows.

The first line of each test case contains \(2\) integers \(n\) and \(k\) (\(2 \le n \le 5 \cdot 10^4\), $1 k $ ).

The second line contains \(2n\) integers \(a_1, a_2, \ldots, a_{2n}\) (\(1 \le a_i \le n\)). It is guaranteed that every integer from \(1\) to \(n\) occurs exactly twice in \(a\).

It is guaranteed that the sum of \(n\) over all test cases does not exceed \(5 \cdot 10^4\).

输入

每个测试包含多个测试用例。第一行包含一个整数 \(t\) (\(1 \leq t \leq 5000\)) — 测试用例的数量。接下来是每个测试用例的描述。

每个测试用例的第一行包含 \(2\) 个整数 \(n\) 和 \(k\) (\(2 \le n \le 5 \cdot 10^4\), $1 k {2} $ )。

第二行包含 \(2n\) 个整数 \(a &#95; 1, a &#95; 2, \ldots, a &#95; {2n}\) (\(1 \le a &#95; i \le n\))。保证 \(a\) 中的每个整数从 \(1\) 到 \(n\) 都恰好出现两次。

保证所有测试用例中 \(n\) 的总和不超过 \(5 \cdot 10^4\)。

Output

For each test case, output two lines.

On the first line of output, output \(2k\) integers \(l_1, l_2, \ldots, l_{2k}\).

On the second line of output, output \(2k\) integers \(r_1, r_2, \ldots r_{2k}\).

If there are multiple solutions, you may output any one of them.

输出

对于每个测试用例，输出两行。

在输出的第一行上，输出\(2k\)个整数\(l &#95; 1, l &#95; 2, \ldots, l &#95; {2k}\)。

在输出的第二行上，输出\(2k\)个整数\(r &#95; 1, r &#95; 2, \ldots r &#95; {2k}\)。

如果存在多个解，你可以输出其中任意一个。

Example

input

4
2 1
1 2 2 1
6 1
6 4 2 1 2 3 1 6 3 5 5 4
4 1
1 2 3 4 1 2 3 4
6 2
5 1 3 3 5 1 2 6 4 6 4 2

output

2 1
2 1
6 4
1 3
1 2
1 2
5 1 3 3
6 4 2 4

Note

In the first test case, we choose \(l=[2,1]\) and \(r=[2,1]\). \([2, 1]\) is a subset of \([a_1, a_2]\) and \([2, 1]\) is a subset of \([a_3, a_4]\), and \(2 \oplus 1 = 2 \oplus 1 = 3\).

In the second test case, \(6 \oplus 4 = 1 \oplus 3 = 2\).

注意

在第一个测试用例中，我们选择 \(l=[2,1]\) 和 \(r=[2,1]\)。\([2, 1]\) 是 \([a &#95; 1, a &#95; 2]\) 的子集，\([2, 1]\) 是 \([a &#95; 3, a &#95; 4]\) 的子集，并且 \(2 \oplus 1 = 2 \oplus 1 = 3\)。

在第二个测试用例中，\(6 \oplus 4 = 1 \oplus 3 = 2\)。

Code1-WA

240317

#include<bits/stdc++.h>
using namespace std;
const int M=50010;
set<int> s;
vector<int> v1,v2;

void solve(){
    // memset(nums,0,sizeof(nums));
    s.clear();
    v1.clear();
    v2.clear();
    stringstream s1,s2;
    int n,k;
    cin>>n>>k;
    int cnt1=0,cnt2=0;
    for(int i=0;i<n;i++){
        int t;
        cin>>t;
        if(s.find(t)!=s.end()){
            s.erase(t);
            v1.emplace_back(t);
        } else s.insert(t);
    }
    for(int i=0;i<n;i++){
        int t;
        cin>>t;
        if(s.find(t)==s.end()) v2.emplace_back(t);
    }
    int vsize=v1.size();
    // cout<<v1.size()<<" "<<v2.size()<<endl;
    for(int i=0;i<min(k,vsize);i++){
        s1<<v1[i]<<" "<<v1[i]<<" ";
    }
    for(int i=0;i<min(k,vsize);i++){
        s2<<v2[i]<<" "<<v2[i]<<" ";
    }
    int cnt=k-vsize;
    cnt*=2;
    // for(auto k:s){
    //     cout<<k<<" ";
    // }cout<<endl;
    for(const int& c:s){
        if(!cnt) break;
        s1<<c<<" ";
        s2<<c<<" ";
        cnt--;
    }
    cout<<s1.str()<<"\n"<<s2.str()<<"\n";





    // vector<int> v1(n),v2(n);
    // int cnt1=n-2*k,cnt2=n-2*k;
    // int xor1,xor2;
    // cin>>v1[0],xor1=v1[0];
    // for(int i=1;i<n;i++) cin>>v1[i],xor1^=v1[i];
    // cin>>v2[0],xor2=v2[0];
    // for(int i=1;i<n;i++) cin>>v2[i],xor2^=v2[i];

    // sort(v1.begin(),v1.end(),greater<int>());
    // sort(v2.begin(),v2.end(),greater<int>());

    // while(xor1^xor2 && cnt1 && cnt2){
    //     int digit=1;
    //     int temp=xor1^xor2;

    // }
}



int main(){
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);
    int t;
    cin>>t;
    while(t--)
    solve();
    return 0;
}

Code2-PreAC

240317

#include<bits/stdc++.h>
using namespace std;
const int M=50010;
set<int> s1,s2,s3;

void solve(){
    // memset(nums,0,sizeof(nums));
    s1.clear(); //共有的
    s2.clear();
    s3.clear();
    stringstream str1,str2;
    int n,k;
    cin>>n>>k;
    int cnt1=0,cnt2=0;
    for(int i=0;i<n;i++){
        int t;
        cin>>t;
        if(s1.find(t)!=s1.end()){
            s1.erase(t);
            s2.insert(t);
        } else s1.insert(t);
    }
    for(int i=0;i<n;i++){
        int t;
        cin>>t;
        if(s1.find(t)==s1.end()) s3.insert(t);
    }
    // for(auto c:s1) cout<<c<<" ";
    // cout<<endl;
    // for(auto c:s2) cout<<c<<" ";
    // cout<<endl;
    // for(auto c:s3) cout<<c<<" ";
    // cout<<endl;
    if(k<=s2.size()){
        int cnt=k;
        for(auto c:s2){
            if(cnt<=0) break;
            str1<<c<<" "<<c<<" ";
            cnt--;
        }
        cnt=k;
        for(auto c:s3){
            if(cnt<=0) break;
            str2<<c<<" "<<c<<" ";
            cnt--;
        }
    }else{
        int cnt=(k-s2.size())*2;
        for(auto c:s2){
            str1<<c<<" "<<c<<" ";
        }
        for(auto c:s3){
            str2<<c<<" "<<c<<" ";
        }
        for(auto c:s1){
            if(cnt<=0) break;
            str1<<c<<" ";
            str2<<c<<" ";
            cnt--;
        }
    }
    cout<<str1.str()<<"\n"<<str2.str()<<"\n";
    // int size=s2.size();
    // int cnt=min(k,size);
    // // cout<<v1.size()<<" "<<v2.size()<<endl;
    // for(const int& num:s1){
    //     if(!cnt) break;
    //     str1<<num<<" "<<num<<" ";
    //     cnt--;
    // }
    // cnt=min(k,size);
    // for(const int& num:s2){
    //     if(!cnt) break;
    //     str2<<num<<" "<<num<<" ";
    //     cnt--;
    // }
    // cnt=k-size;
    // cnt*=2;
    // // for(auto k:s){
    // //     cout<<k<<" ";
    // // }cout<<endl;
    // for(const int& c:v){
    //     if(cnt<=0) break;
    //     str1<<c<<" ";
    //     str2<<c<<" ";
    //     cnt--;
    // }
    // cout<<str1.str()<<"\n"<<str2.str()<<"\n";





    // vector<int> v1(n),v2(n);
    // int cnt1=n-2*k,cnt2=n-2*k;
    // int xor1,xor2;
    // cin>>v1[0],xor1=v1[0];
    // for(int i=1;i<n;i++) cin>>v1[i],xor1^=v1[i];
    // cin>>v2[0],xor2=v2[0];
    // for(int i=1;i<n;i++) cin>>v2[i],xor2^=v2[i];

    // sort(v1.begin(),v1.end(),greater<int>());
    // sort(v2.begin(),v2.end(),greater<int>());

    // while(xor1^xor2 && cnt1 && cnt2){
    //     int digit=1;
    //     int temp=xor1^xor2;

    // }
}



int main(){
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);
    int t;
    cin>>t;
    while(t--)
    solve();
    return 0;
}