LeetCodeEveryday

Coding Everyday

2575. 找出字符串的可整除数组

给你一个下标从 0 开始的字符串 word ，长度为 n ，由从 0 到 9 的数字组成。另给你一个正整数 m 。

word 的 可整除数组 div 是一个长度为 n 的整数数组，并满足：

• 如果 word[0,...,i] 所表示的 数值 能被 m 整除，div[i] = 1
• 否则，div[i] = 0

返回 word 的可整除数组。

示例 1：

输入：word = "998244353", m = 3
输出：[1,1,0,0,0,1,1,0,0]
解释：仅有 4 个前缀可以被 3 整除："9"、"99"、"998244" 和 "9982443" 。

示例 2：

输入：word = "1010", m = 10
输出：[0,1,0,1]
解释：仅有 2 个前缀可以被 10 整除："10" 和 "1010" 。

提示：

• 1 <= n <= 105
• word.length == n
• word 由数字 0 到 9 组成
• 1 <= m <= 109

Code

240307

class Solution {
public:
    vector<int> divisibilityArray(string word, int m) {
        int len=word.length();
        vector<int> res(len);
        long long num=0;
        for(int i=0;i<len;i++){
            num*=10;
            num+=word[i]-'0';
            if(num%m==0) res[i]=1;
            else res[i]=0;
            num%=m;
        }
        return res;
    }
};

class Solution:
    def divisibilityArray(self, word: str, m: int) -> List[int]:
        length=len(word)
        res=[0]*length
        num=0
        for i in range(0,length):
            num*=10
            num+=int(word[i])
            if(num%m==0):
                res[i]=1
            else:
                res[i]=0
            num%=m
        return res

2834. 找出美丽数组的最小和

给你两个正整数：n 和 target 。

如果数组 nums 满足下述条件，则称其为 美丽数组 。

• nums.length == n.
• nums 由两两互不相同的正整数组成。
• 在范围 [0, n-1] 内，不存在 两个 不同 下标 i 和 j ，使得 nums[i] + nums[j] == target 。

返回符合条件的美丽数组所可能具备的 最小 和，并对结果进行取模 109 + 7。

示例 1：

输入：n = 2, target = 3
输出：4
解释：nums = [1,3] 是美丽数组。
- nums 的长度为 n = 2 。
- nums 由两两互不相同的正整数组成。
- 不存在两个不同下标 i 和 j ，使得 nums[i] + nums[j] == 3 。
可以证明 4 是符合条件的美丽数组所可能具备的最小和。

示例 2：

输入：n = 3, target = 3
输出：8
解释：
nums = [1,3,4] 是美丽数组。 
- nums 的长度为 n = 3 。 
- nums 由两两互不相同的正整数组成。 
- 不存在两个不同下标 i 和 j ，使得 nums[i] + nums[j] == 3 。
可以证明 8 是符合条件的美丽数组所可能具备的最小和。

示例 3：

输入：n = 1, target = 1
输出：1
解释：nums = [1] 是美丽数组。

提示：

• 1 <= n <= 109
• 1 <= target <= 109

Code1

240308

超时，n=1000000000 target=1000000000。

class Solution {
public:
    const int MOD=1000000007;
    int minimumPossibleSum(int n, int target) {
        int sum=0;
        int last=min(target/2,n);
        for(int i=1;i<=last;i++){
            sum=(sum+i)%MOD;
            // cout<<i<<",";
        }
        last=target+n-min(target/2,n);
        for(int i=target;i<last;i++){
            sum=(sum+i)%MOD;
            // cout<<target<<",";
        }
        // cout<<endl;
        return sum;
    }
};

Code2

240308

数学题，优化成O(1)了。

class Solution {
public:
    const int MOD=1000000007;
    int minimumPossibleSum(int n, int target) {
        long long sum=0;
        long long last=min(target/2,n);
        sum=(1+last)*last/2;
        last=target+n-min(target/2,n);
        sum+=(target+last-1)*(last-target)/2;
        return sum%MOD;
    }
};

class Solution {
public:
    int minimumPossibleSum(int n, int target) {
        long long Min=min(target/2,n);
        return ((Min+1)*Min/2+((long long)target+target+n-Min-1)*(n-Min)/2)%1000000007;
    }
};

class Solution:
    def minimumPossibleSum(self, n: int, target: int) -> int:
        temp=min(n,target//2)
        sum=(1+temp)*temp//2
        temp=target+n-temp
        sum+=(target+temp-1)*(temp-target)//2
        return sum%1000000007
        # if(n<=target//2):
        #     res=(1+n)*n//2
        #     return res%1000000007
        # else:
        #     res=(1+target//2)*target//4
        #     res+=(target+target+(n-target//2)-1)*(n-target//2)//2
        #     return res%1000000007

2386. 找出数组的第 K 大和

给你一个整数数组 nums 和一个 正 整数 k 。你可以选择数组的任一 子序列 并且对其全部元素求和。

数组的 第 k 大和 定义为：可以获得的第 k 个 最大 子序列和（子序列和允许出现重复）

返回数组的 第 k 大和 。

子序列是一个可以由其他数组删除某些或不删除元素排生而来的数组，且派生过程不改变剩余元素的顺序。

注意：空子序列的和视作 0 。

示例 1：

输入：nums = [2,4,-2], k = 5
输出：2
解释：所有可能获得的子序列和列出如下，按递减顺序排列：
- 6、4、4、2、2、0、0、-2
数组的第 5 大和是 2 。

示例 2：

输入：nums = [1,-2,3,4,-10,12], k = 16
输出：10
解释：数组的第 16 大和是 10 。

提示：

• n == nums.length
• 1 <= n <= 105
• -109 <= nums[i] <= 109
• 1 <= k <= min(2000, 2n)

Code

240309

超时，时间复杂度\(O(nk)\)。

class Solution {
public:
    void debug(priority_queue<long long,vector<long long>,greater<long long>> q){
        while(!q.empty()){
            cout<<q.top()<<",";
            q.pop();
        }
        cout<<endl;
    }
    long long kSum(vector<int>& nums, int k) {
        sort(nums.begin(),nums.end(),greater<int>());
        priority_queue<long long,vector<long long>,greater<long long>> q;
        priority_queue<long long,vector<long long>,greater<long long>> temp;
        for(int num:nums){
            // if(num<0 && q.size()>=k) break;
            temp=q;
            while(!temp.empty()){
                q.emplace(temp.top()+num);
                temp.pop();
            }
            q.emplace(num);
            // debug(q);
            while(q.size()>k){
                q.pop();
            }
            // cout<<q.size()<<endl;
            // debug(q);
            // cout<<endl;
        }
        q.emplace(0);
        while(q.size()>k) q.pop();
        // debug(q);
        return q.top();
    }
};

Code2

230309

做不来了。。。

2129. 将标题首字母大写

给你一个字符串 title ，它由单个空格连接一个或多个单词组成，每个单词都只包含英文字母。请你按以下规则将每个单词的首字母 大写 ：

• 如果单词的长度为 1 或者 2 ，所有字母变成小写。
• 否则，将单词首字母大写，剩余字母变成小写。

请你返回 大写后 的 title 。

示例 1：

输入：title = "capiTalIze tHe titLe"
输出："Capitalize The Title"
解释：
由于所有单词的长度都至少为 3 ，将每个单词首字母大写，剩余字母变为小写。

示例 2：

输入：title = "First leTTeR of EACH Word"
输出："First Letter of Each Word"
解释：
单词 "of" 长度为 2 ，所以它保持完全小写。
其他单词长度都至少为 3 ，所以其他单词首字母大写，剩余字母小写。

示例 3：

输入：title = "i lOve leetcode"
输出："i Love Leetcode"
解释：
单词 "i" 长度为 1 ，所以它保留小写。
其他单词长度都至少为 3 ，所以其他单词首字母大写，剩余字母小写。

Code

240311

class Solution {
public:
    string capitalizeTitle(string title) {
        stringstream ss(title);
        string word,res;
        while(ss>>word){
            if(word.length()<=2){
                for(char& c:word){
                    c=tolower(c);
                }
                res+=word+" ";
            }else{
                for(char& c:word) c=tolower(c);
                word[0]=toupper(word[0]);
                res+=word+" ";
            }
        }
        res.pop_back();
        return res;
    }
};

2684. 矩阵中移动的最大次数

给你一个下标从 0 开始、大小为 m x n 的矩阵 grid ，矩阵由若干 正 整数组成。

你可以从矩阵第一列中的 任一 单元格出发，按以下方式遍历 grid ：

• 从单元格 (row, col) 可以移动到 (row - 1, col + 1)、(row, col + 1) 和 (row + 1, col + 1) 三个单元格中任一满足值 严格 大于当前单元格的单元格。

返回你在矩阵中能够 移动 的 最大 次数。

示例 1：

img

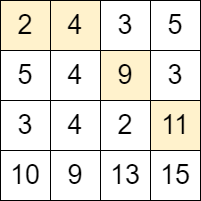
输入：grid = [[2,4,3,5],[5,4,9,3],[3,4,2,11],[10,9,13,15]]
输出：3
解释：可以从单元格 (0, 0) 开始并且按下面的路径移动：
- (0, 0) -> (0, 1).
- (0, 1) -> (1, 2).
- (1, 2) -> (2, 3).
可以证明这是能够移动的最大次数。

示例 2：

输入：grid = [[3,2,4],[2,1,9],[1,1,7]]
输出：0
解释：从第一列的任一单元格开始都无法移动。

提示：

• m == grid.length
• n == grid[i].length
• 2 <= m, n <= 1000
• 4 <= m * n <= 105
• 1 <= grid[i][j] <= 106

Code

240316

class Solution {
public:

    int Max,m,n;
    // void bfs(vector<vector<int>>& matrix,int xx){
    //     queue<pair<int,int>> q;
    //     // vector<vector<int>> vis(m,vector<int>(n,0));
    //     q.push({xx,0});
    //     // vis[xx][0]=1;
    //     while(!q.empty()){
    //         int x=q.front().first;
    //         int y=q.front().second;
    //         // cout<<x<<","<<y<<endl;
    //         Max=max(Max,y);
    //         q.pop();
    //         for(int i=-1;i<=1;i++){
    //             if(x+i>=0 && x+i<m && y+1<n && matrix[x+i][y+1]>matrix[x][y]){
    //                 // vis[x+i][y+1]=1;
    //                 q.push({x+i,y+1});
    //             }
    //         }
    //     }
    // }
    int maxMoves(vector<vector<int>>& grid) {
        m=grid.size();
        n=grid[0].size();
        Max=0;
        // for(int i=0;i<m;i++){
        //     bfs(grid,i);
        // }
        queue<pair<int,int>> q;
        vector<vector<int>> vis(m,vector<int>(n,0));
        for(int i=0;i<m;i++){
            q.push(make_pair(i,0));
        }
        // vis[xx][0]=1;
        while(!q.empty()){
            int x=q.front().first;
            int y=q.front().second;
            // cout<<x<<","<<y<<endl;
            Max=max(Max,y);
            q.pop();
            for(int i=-1;i<=1;i++){
                if(x+i>=0 && x+i<m && y+1<n && grid[x+i][y+1]>grid[x][y] && !vis[x+i][y+1]){
                    vis[x+i][y+1]=1;
                    q.push({x+i,y+1});
                }
            }
        }
        return Max;
    }
};

303. 区域和检索 - 数组不可变

给定一个整数数组 nums，处理以下类型的多个查询:

1. 计算索引 left 和 right （包含 left 和 right）之间的 nums 元素的 和 ，其中 left <= right

实现 NumArray 类：

• NumArray(int[] nums) 使用数组 nums 初始化对象
• int sumRange(int i, int j) 返回数组 nums 中索引 left 和 right 之间的元素的 总和 ，包含 left 和 right 两点（也就是 nums[left] + nums[left + 1] + ... + nums[right] )

示例 1：

输入：
["NumArray", "sumRange", "sumRange", "sumRange"]
[[[-2, 0, 3, -5, 2, -1]], [0, 2], [2, 5], [0, 5]]
输出：
[null, 1, -1, -3]

解释：
NumArray numArray = new NumArray([-2, 0, 3, -5, 2, -1]);
numArray.sumRange(0, 2); // return 1 ((-2) + 0 + 3)
numArray.sumRange(2, 5); // return -1 (3 + (-5) + 2 + (-1)) 
numArray.sumRange(0, 5); // return -3 ((-2) + 0 + 3 + (-5) + 2 + (-1))

提示：

• 1 <= nums.length <= 104
• -105 <= nums[i] <= 105
• 0 <= i <= j < nums.length
• 最多调用 104 次 sumRange 方法

Code

240318

class NumArray {
public:
    vector<int> v;
    NumArray(vector<int>& nums) {
        int n=nums.size();
        v.resize(n,0);
        v[0]=nums[0];
        for(int i=1;i<n;i++){
            v[i]=v[i-1]+nums[i];
        }
    }
    
    int sumRange(int left, int right) {
        if(left==0) return v[right];
        else return v[right]-v[left-1];
    }
};

/**
 * Your NumArray object will be instantiated and called as such:
 * NumArray* obj = new NumArray(nums);
 * int param_1 = obj->sumRange(left,right);
 */